Estoy intentando resolver este ejercicio hace tiempo porque me sigue dando un resultado distinto al del archivo de soluciones. Verán, como el ascensor está subiendo y es opuesta (sentido opuesto) a la gravedad, me estoy tomando como el peso de la masita como m(-g+a) = m(a-g) por un tema de sistema de referencia; como la aceleración es para arriba y la gravitatoria para abajo (o viceversa si te tomas el sistema de referncia para "abajo" positivo y "arriba" negativo). En fin, esa es la discordancia y porque no me está dando lo mismo que la solución. Necesito saber que es lo que está mal, si yo no estoy considerando algo o está mal en la hoja de respuestas. Gracias
Buenas,
La intuición que tuviste de agregar un término de aceleración es correcta, pero quizá plantear las ecuaciones sin pensar en esto es más fácil para evitar errores de signos. Si planteamos Newton en el eje 
obtenemos:
Un término de 
, uno por la gravedad y en el lado derecho, como siempre 
, siendo 
la del ejercicio. Si pasamos el término hacia la izquierda
Vemos que terminan como un sólo término teniendo 
y el mismo signo. Esto es coherente si uno piensa en el caso en que está en un ascensor. Al subir pesamos más, por lo que uno esperaría que las cuentas nos den términos con el mismo signo.
Además, podemos pensar un caso un poco raro, pero que sirve para ilustrar el caso anterior. Si estuviéramos en ese mismo ascensor pero ignorando la gravedad (o en una nave que acelera en el espacio, por ejemplo) los objetos caerían al suelo de manera similar a como lo hacen en la tierra. Al sumarle a esta situación la gravedad, los objetos caerían más rápidos.
Por fuera del ejercicio, es interesante ver el caso en que la aceleración ahora es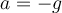 
. La ecuación queda
La tensión nos queda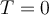 
. Eso tiene sentido? Bueno, estamos analizando el caso en que el ascensor esta bajando a 
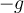, ósea, está en caída libre, por lo que es coherente que la cuerda no esté tensa!
Saludos!
Ahora si pude resolverlo, muchas gracias!