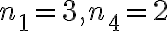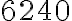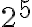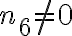Sobre el Practico#03

Estuve trabajando sobre este problema y creo que logré hallar una solución, pero me quedaron unas cuentas larguísimas.

Básicamente, planteé el teorema multinomial para el caso concreto: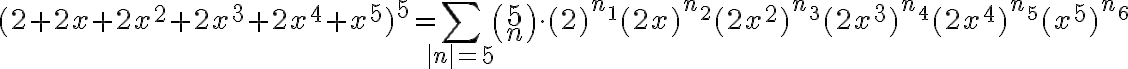

$(2 + 2x + 2x^2 + 2x^3 + 2x^4 + x^5)^5 = \sum_{|n| = 5} \binom{5}{n} \cdot (2)^{n_1}(2x)^{n_2}(2x^2)^{n_3}(2x^3)^{n_4}(2x^4)^{n_5}(x^5)^{n_6}$

simplificando llegué a: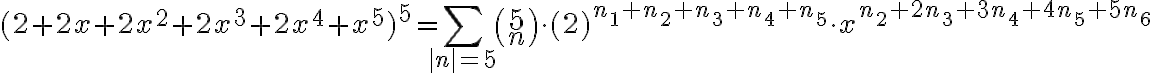

$(2 + 2x + 2x^2 + 2x^3 + 2x^4 + x^5)^5 = \sum_{|n| = 5} \binom{5}{n} \cdot (2)^{n_1 + n_2 + n_3 + n_4 + n_5} \cdot x^{n_2 + 2n_3 + 3n_4 + 4n_5 + 5n_6}$

y de ahí salen las dos ecuaciones que deben cumplir los exponentes: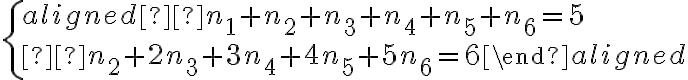

$\left\{\begin{aligned}   n_1 + n_2 + n_3 + n_4 + n_5 + n_6 = 5 \\  n_2 + 2n_3 + 3n_4 + 4n_5 + 5n_6 = 6\end{aligned}\right.$

Cada solución de ese sistema aporta un sumando. El tema es que resolverlo me resulta bastante complicado. La otra parte de este ejercicio y otros similares que han aparecido en prácticos de otros años son más cortos, por lo que, mirando con atención, uno más o menos saca todas las soluciones. ¿Hay algún método para resolver esto de forma más sistemática?

Por si le sirve a alguien más, las soluciones que obtuve fueron (los $n$ que no aparecen son $0$):

$\left\{\begin{aligned}  &n_1 = 3,\ \phantom{n_2 = 0,} n_3 = 1,\ \phantom{n_4 = 0,} n_5 = 1,\ \phantom{n_6 = 0} \\  &n_1 = 2,\ \phantom{n_2 = 0,} n_3 = 3,\ \phantom{n_4 = 0,}\phantom{n_5 = 0,}\phantom{n_6 = 0} \\  &n_1 = 3,\ n_2 = 1,\ \phantom{n_3 = 0,}\phantom{n_4 = 0,}\phantom{n_5 = 0,}n_6 = 1 \\  &n_1 = 2,\ n_2 = 1,\ n_3 = 1,\ n_4 = 1,\ \phantom{n_5 = 0,}\phantom{n_6 = 0} \\  &n_1 = 2,\ n_2 = 2,\ \phantom{n_3 = 0,}\phantom{n_4 = 0,}n_5 = 1,\ \phantom{n_6 = 0} \\  &n_1 = 1,\ n_2 = 2,\ n_3 = 2,\ \phantom{n_4 = 0,}\phantom{n_5 = 0,}\phantom{n_6 = 0} \\  &n_1 = 1,\ n_2 = 3,\ \phantom{n_3 = 0,} n_4 = 1,\ \phantom{n_5 = 0,}\phantom{n_6 = 0} \\  &\phantom{n_1 = 0,\ }n_2 = 4,\ n_3 = 1,\ \phantom{n_4 = 0,}\phantom{n_5 = 0,}\phantom{n_6 = 0,}\end{aligned}\right.$

Que terminan dando la suma:

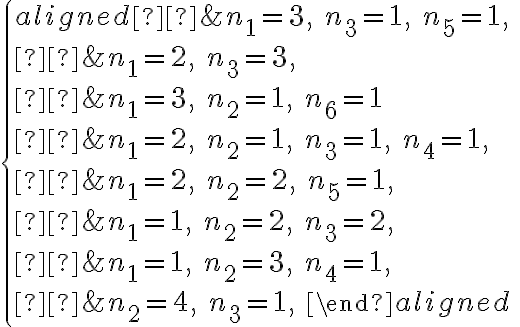
$[x^6] = {5! \over 3!} \cdot 2^5 + {5!\over 2!\cdot 3!} \cdot 2^5 + {5!\over 3!} \cdot 2^5 + {5!\over 2!} \cdot 2^5 + {5!\over 2!\cdot 2!} \cdot 2^5 + {5!\over 2!\cdot 2!} \cdot 2^5 + {5!\over 3!} \cdot 2^5 + {5!\over 4!} \cdot 2^5 = 6240$