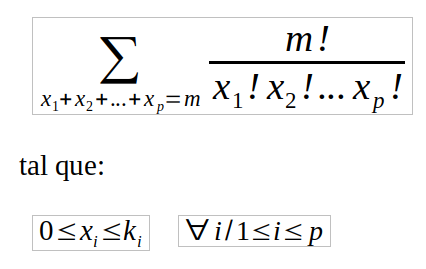Hola. Tengo una duda acerca de los casos contemplados en el teórico. Se ha visto permutaciones y combinaciones con y sin repetición. Luego hay un caso que entra dentro de permutaciones con repetición que sería teniendo un conjunto de n elementos, donde tengo k1 elementos de tipo1, k2 de tipo2 y así hasta kp de tipop, donde la suma de k1+k2+..+kp=n.
Si quiero extraer dichos n elementos y me importa el orden, la fórmula para el conteo sería: n!/(k1!....kp!).
Ahora bien, si en lugar de n, quiero extraer m elementos donde m<n, no sé si fue visto en teórico o es trivial pero no me doy cuenta tan directamente.
Gracias.