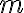Hola. Tengo una duda acerca de la demostración expuesta por Alexandre en el segundo teórico de Inducción Completa (en el min. 1:20 del video aprox.).
Allí se busca demostrar por el absurdo y utilizando el principio de buen orden, que todo Natural mayor o igual a 2 se puede descomponer en el producto de dos números primos.
En la demostración se utiliza m=p*q donde p y q son menores que m, o sea no pertenecen al conjunto A. Aquí es donde me surge la duda: se afirma que p y q se pueden descomponer en el producto de números primos por no pertenecer a A. Mi duda es cómo se puede afirmar esto si es justamente lo que quiero probar?
Desde ya gracias y disculpas si no fue clara la redacción.
Saludos,
Fernando.