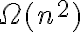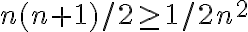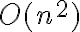Buenas, no me queda claro como se termina de demostrar el ejercicio, ya que en el monitoreo se terminó la explicación con el ejemplo y la cantidad de iteraciones en el mismo. Llegamos a (n x (n + 1))/2 y de ahi directamente se dedujo que el tiempo del peor caso es Omega(n cuadrado), lo cual no entendí la explicación.
Saludos.