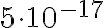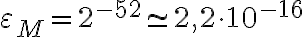Practico 1. Ejercicio 4, parte c)

Practico 1. Ejercicio 4, parte c)

de Diego Furrer Dellepiane -
Número de respuestas: 5

Buenas! Espero se encuentren bien.

Vi la solución del examen y me generó una duda. 


Simplemente dice que 1-5x10^-17 se redondea a 1 en precisión doble, pero no explica el porqué.

Yo calculé la distancia entre los números representables entre el 1/2 y 1, me dio 2^-53 que es aproximadamente 1.1x10^-16. Entonces si lo que le resto es menor a la mitad de esa distancia, el valor se redondea a 1.

En este caso le queremos restar 5x10^-17 y la mitad de la distancia es 5.5x10^-17, entonces como lo que le queremos restar es menor a la mitad de la distancia, y como se aplica redondeo, el número resultado es 1.

1. Esta explicación es correcta?
2. Es necesaria? O simplemente con decir que en punto flotante se redondea a 1 es suficiente?

Muchas gracias!

Saludos,

Diego Furrer.





En respuesta a Diego Furrer Dellepiane

Re: Practico 1. Ejercicio 4, parte c)

de Pablo Zadkiel Alfano Patron -

Pasa que 5\cdot 10^{-17} es más chico que \varepsilon_M = 2^{-52} \simeq 2,2\cdot 10^{-16} , entonces ocurre el redondeo.
En respuesta a Pablo Zadkiel Alfano Patron

Re: Practico 1. Ejercicio 4, parte c)

de Diego Furrer Dellepiane -

Buenas! Gracias por la respuesta Pablo.

Tengo entendido que el Épsilon de máquina es la separación entre 1 y el siguiente número representable.

Sin embargo, estamos yendo hacia el otro lado en este caso, ya que no se trata del siguiente, se trata del anterior por estar restándole.

En cada intervalo ( {... [1/2 , 1), [1,2) , [2,4) ... } ) la distancia entre dos números representables es distinta a en otro intervalo. En este caso estamos en el intervalo [1/2 , 1) , ya que le queremos restar algo a 1.

En este intervalo la distancia entre dos números es de 2^-53 que es aproximadamente 1.1x10^-16.

Ahora, si yo a 1 le restara mas de la mitad de este número mencionado anteriormente, el redondeo se iría para el numero representable anterior a 1, por lo que necesito que lo que le resto sea menor a la mitad de ese número. Es decir, 5.5x10^-17.

Entonces la justificación que entiendo yo correcta es que 5x10^-17 es menor que 5.5x10^-17, y por eso ocurre el redondeo hacia 1.

Así es mi razonamiento y por eso no comparto con lo que decís. 

Pero, perfectamente me puedo haber equivocado en mi razonamiento, por eso voy a esperar a la respuesta de un profesor para que me indiquen en que parte del razonamiento me equivoqué.

Muchas gracias igualmente por responder.

Saludos,

Diego Furrer.



En respuesta a Diego Furrer Dellepiane

Re: Practico 1. Ejercicio 4, parte c)

de Ignacio Bustamante -
Hola Diego,

Es como tal y como decís. Tu explicación es correcta, y es la razón por la cual se redondea a 1. No puedo contestarte la pregunta de la necesidad, porque depende de en qué caso la estés contestando. En el caso de un examen hay diferentes criterios que pueden establecerse y por lo tanto dependería de eso. Lo importante es que la explicación que diste es correcta, y que entendiste bien el motivo por el cual el redondeo ocurre.

Saludos!
En respuesta a Ignacio Bustamante

Re: Practico 1. Ejercicio 4, parte c)

de Diego Furrer Dellepiane -
Buenas! Muchas gracias por la respuesta.

Quería consultar otro tema. En este caso la resta entre 1 y otro número menor que 1/2.
Es un caso muy particular ya que tenemos dos certezas:
- El número 1 es representable en PF
- La resta cae en el intervalo [1/2 , 1)

Ahora, si tengo otra resta del estilo (5x10^-4)-(2x10^-12), en este caso debería:
a) Fijarme el número representable "x" en el que cae el 5x10^-4
b) Fijarme en que intervalo caería la resta : x-(2x10^-12)
c) Calcular la distancia entre dos números representables en ese intervalo
d) Fijarme si 2x10^-12 es menor a la mitad de la distancia obtenida en el paso anterior

Preguntas :
1) Recién haciendo todo esto podría responder la pregunta de si un número es ignorado en una resta?
2) El paso a) es necesario? Yo entiendo que es necesario ya que debemos saber desde donde "arranca" la resta realmente para poder saber el intervalo en el que cae
3) Hay alguna formula para hacer esto más rápido?

Muchas gracias por tu tiempo.

Saludos,

Diego Furrer.
En respuesta a Diego Furrer Dellepiane

Re: Practico 1. Ejercicio 4, parte c)

de Ignacio Bustamante -
El paso a) no es necesario, pero ayuda en caso de que las magnitudes sean muy diferentes entre sí. En tu caso por ejemplo, los exponentes son claramente diferentes y si hay un problema va a estar en qué tan distantes son los números desde tu "x". En general, la pregunta que importa es simplemente dónde cae fl(x) - fl(y). Una vez tenés calculados los dos flotantes, restarlos es un tema de rutina, y solo vas a poder ignorar fl(y) si el exponente de x es "mucho mayor" que el exponente de "y". No se me ocurre una forma sencilla de hacerlo más rápido, dado que es un tema de escala y siempre vas a tener que pasar por algún tipo de comparación, ya sea entre la escala de los dos flotantes o entre la escala del epsilon de máquina estirado (o contraído) por el exponente correspondiente.

Saludos!