Buenas, tengo la siguiente consulta.
En la resolucion brindada en el EVA para este ejercicio muestra lo siguiente:
El dibujo anterior entiendo que quiere decir que realmin es mas grande que 1,25 x 10^-10, ¿verdad?
Sin embargo realmin en precisión simple es 1,18 x 10^-38, lo cual estaria contradiciendo lo anterior
¿Me podrian aclarar el por qué es que se da este problema en precisión simple y no en precisión doble en octave?
Muchas gracias!
Hola Joaquin,
El dibujo es solo una representación de un comportamiento similar a lo que esta pasando. Como dije en clase, no está comparando exactamente con realmin.
La cuenta que está haciendo la computadora es otra y un poco más complicada de explicar, por eso está todo entre comillas. Acá va mi intento de ser más preciso: al evaluar , primero calcula
, primero calcula  . Luego hace la resta.
. Luego hace la resta.
En este caso, al evaluar seno de y en precisión simple y=single(5e-4) le queda:


Es decir, son el mismo número, por lo que la resta da 0. En otras palabras, está haciendo que sin(y) sea igual a y, y "olvidándose" del termino en y^3 por ejemplo, como si estuviera en el rango (0, realmin).
El dibujo es solo una representación de un comportamiento similar a lo que esta pasando. Como dije en clase, no está comparando exactamente con realmin.
La cuenta que está haciendo la computadora es otra y un poco más complicada de explicar, por eso está todo entre comillas. Acá va mi intento de ser más preciso: al evaluar
 , primero calcula
, primero calcula  . Luego hace la resta.
. Luego hace la resta.En este caso, al evaluar seno de y en precisión simple y=single(5e-4) le queda:


Es decir, son el mismo número, por lo que la resta da 0. En otras palabras, está haciendo que sin(y) sea igual a y, y "olvidándose" del termino en y^3 por ejemplo, como si estuviera en el rango (0, realmin).
La cosa es que no está comparando exactamente con el real min, porque la resta  está ocurriendo relativamente lejos de 0, y ahí la precisión es menor. Si pensaráramos que el número es lo suficientemente chico, es decir el y^3 estuviera entre el 0 y el realmin, pasaría lo mismo: el número sería "empujado" a cero.
está ocurriendo relativamente lejos de 0, y ahí la precisión es menor. Si pensaráramos que el número es lo suficientemente chico, es decir el y^3 estuviera entre el 0 y el realmin, pasaría lo mismo: el número sería "empujado" a cero.
La diferencia acá es que primero "empuja" a y a
y a 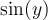 al mismo número (5.0000002e-04) y al restarlos ya da 0.
al mismo número (5.0000002e-04) y al restarlos ya da 0.
En precisión doble, es


y al hacer la resta,

Es decir, no son el mismo número y la resta aún cae en el rango que puede distinguir. Probá repetir esto en Octave para practicar.
Espero se entienda, sino preguntame e intento aclarar.
Saludos!
 está ocurriendo relativamente lejos de 0, y ahí la precisión es menor. Si pensaráramos que el número es lo suficientemente chico, es decir el y^3 estuviera entre el 0 y el realmin, pasaría lo mismo: el número sería "empujado" a cero.
está ocurriendo relativamente lejos de 0, y ahí la precisión es menor. Si pensaráramos que el número es lo suficientemente chico, es decir el y^3 estuviera entre el 0 y el realmin, pasaría lo mismo: el número sería "empujado" a cero.La diferencia acá es que primero "empuja" a
 y a
y a 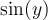 al mismo número (5.0000002e-04) y al restarlos ya da 0.
al mismo número (5.0000002e-04) y al restarlos ya da 0. En precisión doble, es


y al hacer la resta,

Es decir, no son el mismo número y la resta aún cae en el rango que puede distinguir. Probá repetir esto en Octave para practicar.
Espero se entienda, sino preguntame e intento aclarar.
Saludos!
Quedó clarísimo.
Muchas gracias!
Muchas gracias!