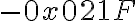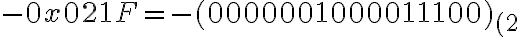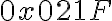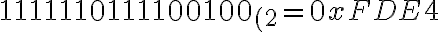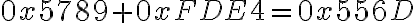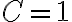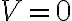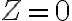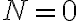Buenas noches,
Voy a poner el ejercicio a) para ver si coincidimos ya que no sé si estoy interpretando bien los parámetros Z, N, C y V.
suma de 0x2977 y 0x5689
los paso a binario (16 bits): 0010 1001 0111 0111
+ 0101 0110 1000 1001
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
1000 0000 0000 0000
Como el número supera el límite 32768 (al ser negativo) entiendo que existe overflow, por lo tanto, V = 1.
A su vez, el bit significativo es 1, por lo que es negativo, N = 1.
Lo que no estoy muy seguro es Z y C... entiendo que Z = 0 porque la suma no da cero, es así?
y con respecto a C, el último bit de acarreo es 1, ya que arrastra el 1 hasta el final, entonces: C = 1??
Espero su ayuda.
Gracias!
Saludos
Gonzalo