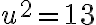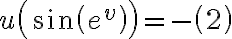En este ejercicio, el primer paso que hice fue hallar (u,v)/ φ(u,v) = (13, -2 , 1)
Hay que resolver el siguiente sistema:
3|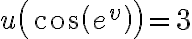
Lo primero que se desprende de la ecuación 1 es que 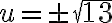
Si uno despeja de la segunda ecuación y llega a :
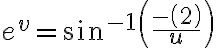
Por lo tanto u queda determinado como 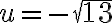
Entonces despejando v este queda : 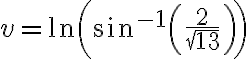
y si con este u y ese v verificamos la tercer ecuación, no llegamos a una igualdad.
Por otro lado, supongamos que ahora despejamos de la tercer ecuación en lugar de la segunda.
Sabemos que 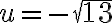
Entonces despejando v de la tercer ecuación queda 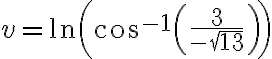
y esta solución si verifica la tercer ecuación.
Entonces mi pregunta es, ¿El sistema tiene solución y es la segunda pareja? ¿No importa que la primer solución no sea válida?