Hola estaba haciendo el ejercicio y al final del todo me quedaba un u cuadrado que para despejar y necesitaba sacarmelo de encima e hice una bhaskara. Es correcto mi procedimiento?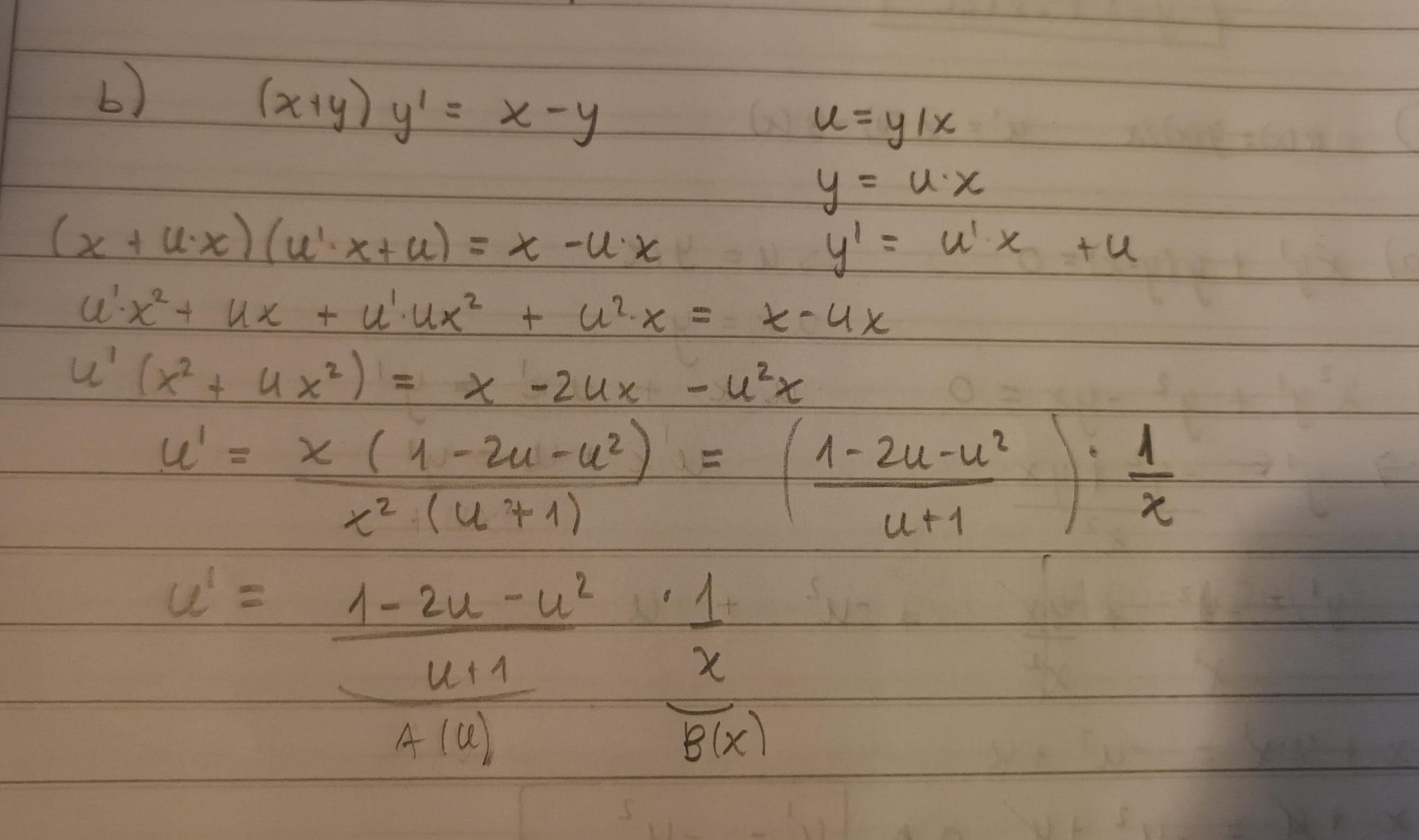
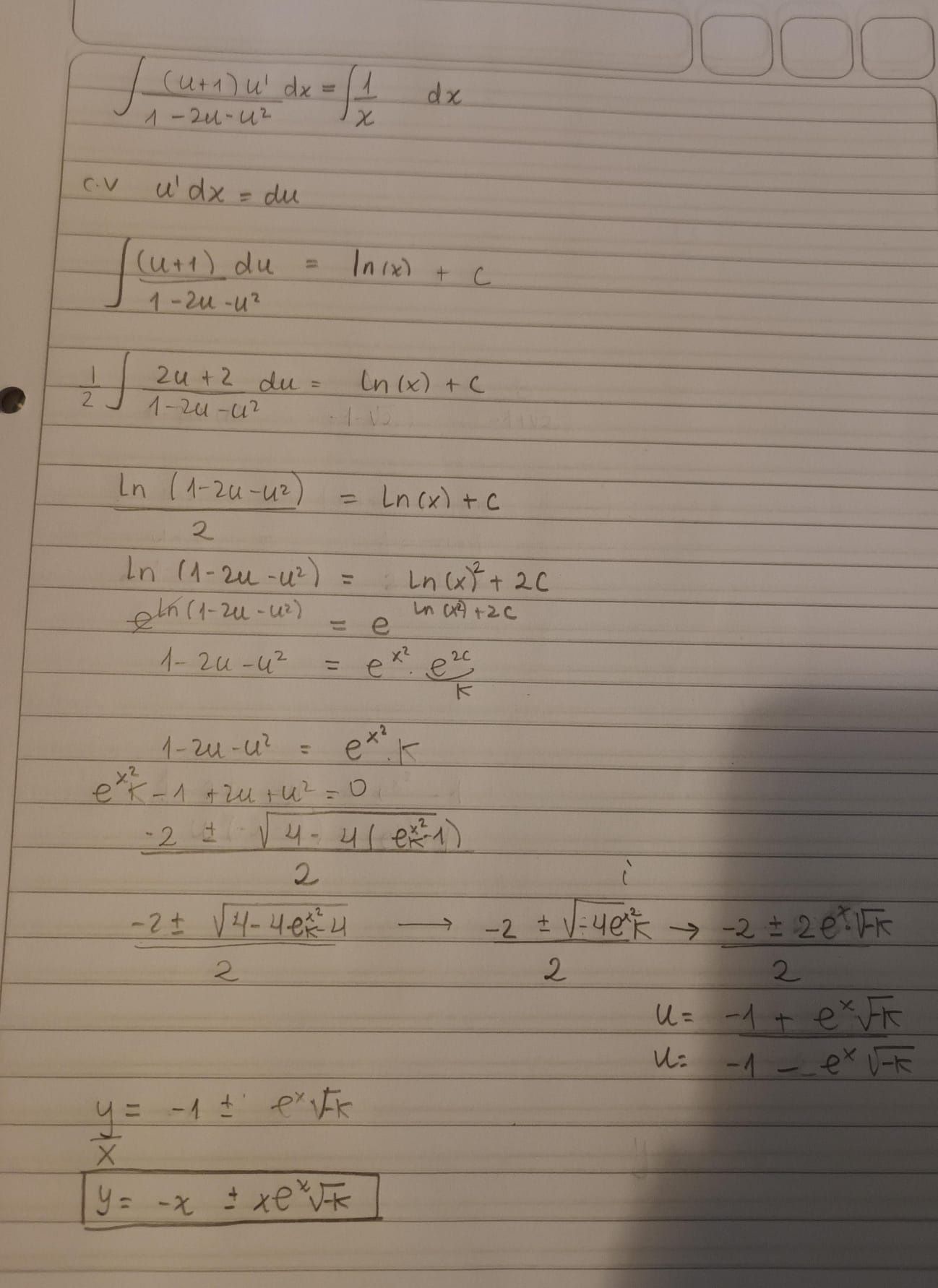
Hola estaba haciendo el ejercicio y al final del todo me quedaba un u cuadrado que para despejar y necesitaba sacarmelo de encima e hice una bhaskara. Es correcto mi procedimiento?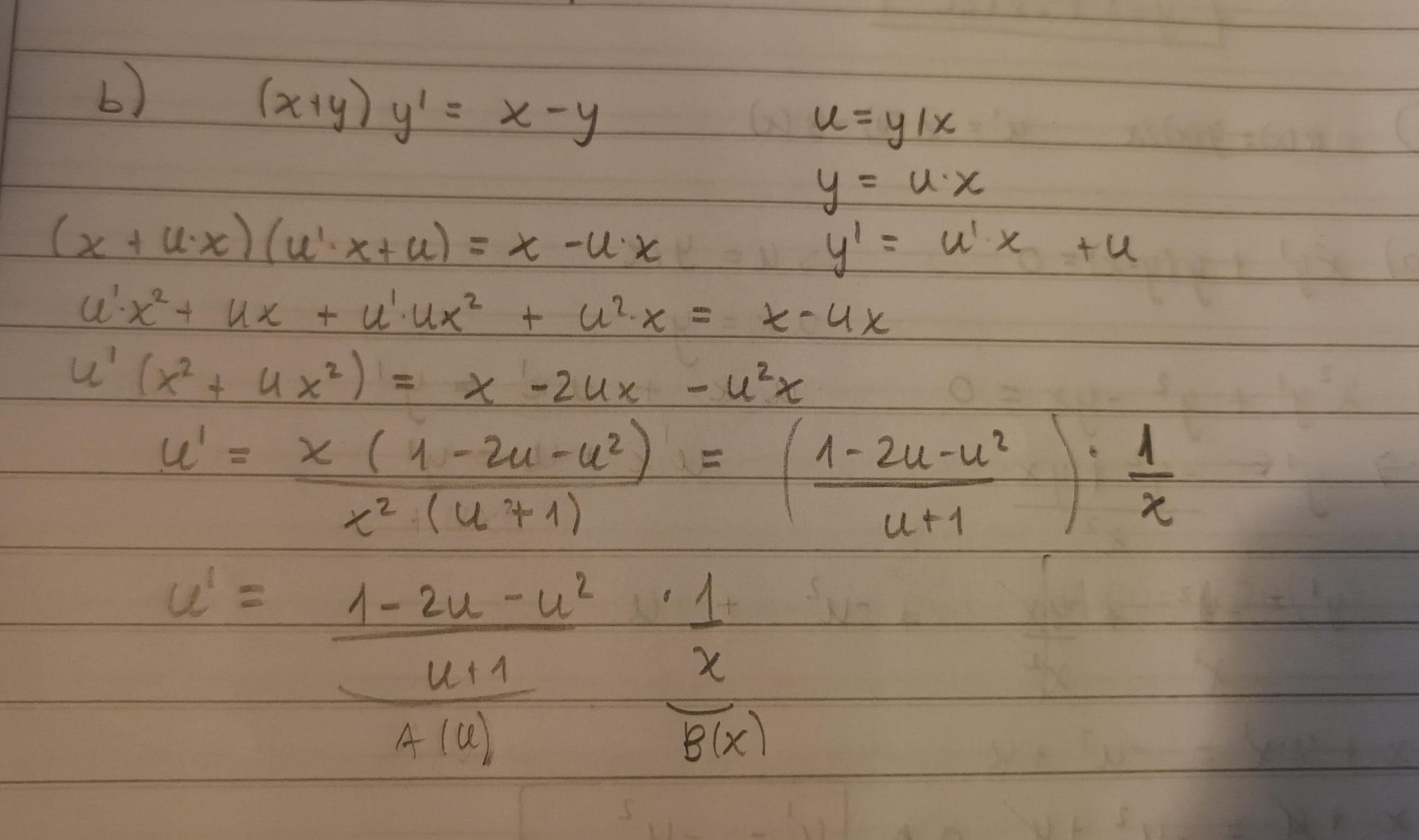
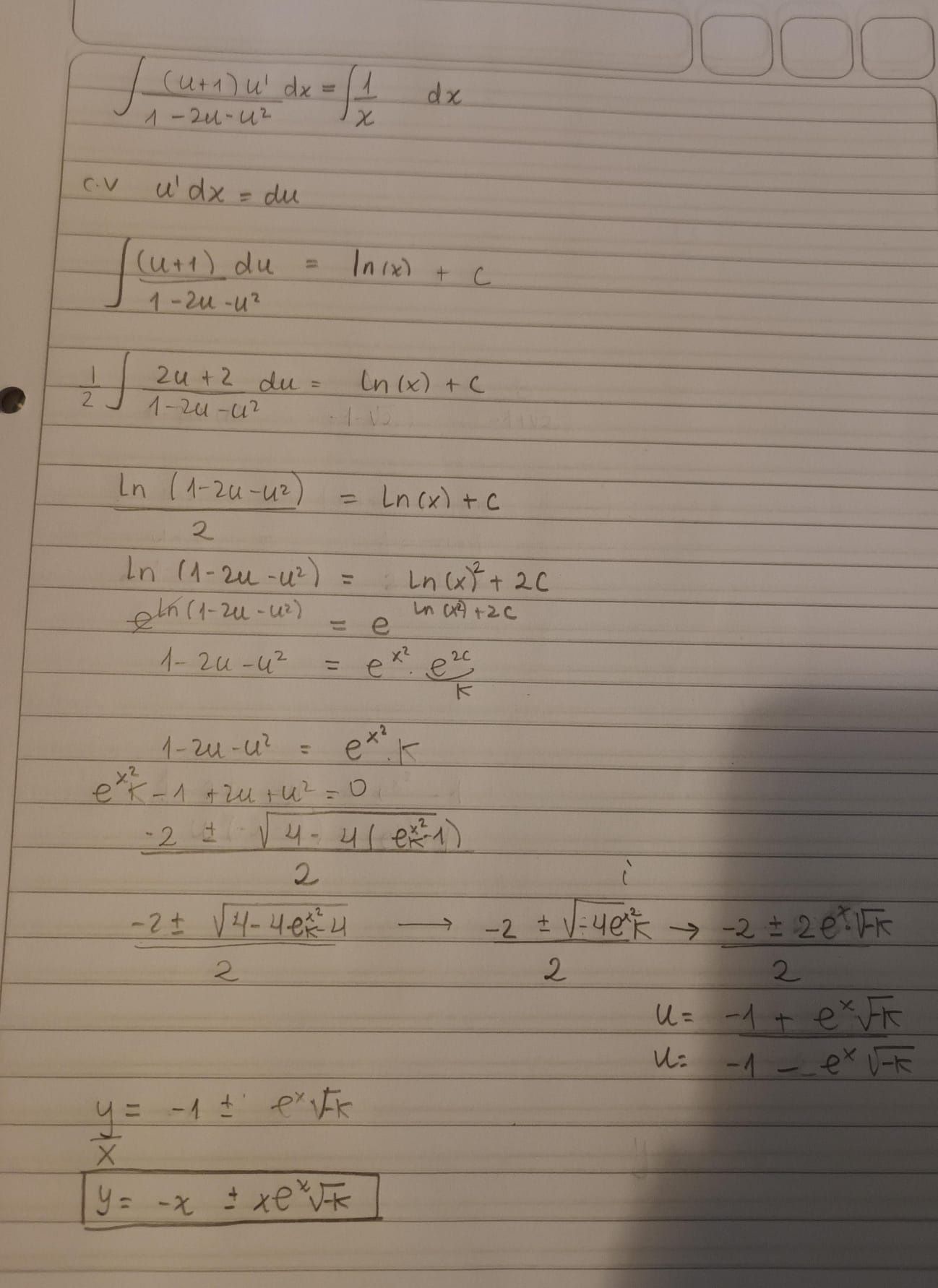
Hola profe, ahi arregle el tema del signo e hice su sugerencia, ahora esta correcto?
Desde ya , muchas gracias por la ayuda
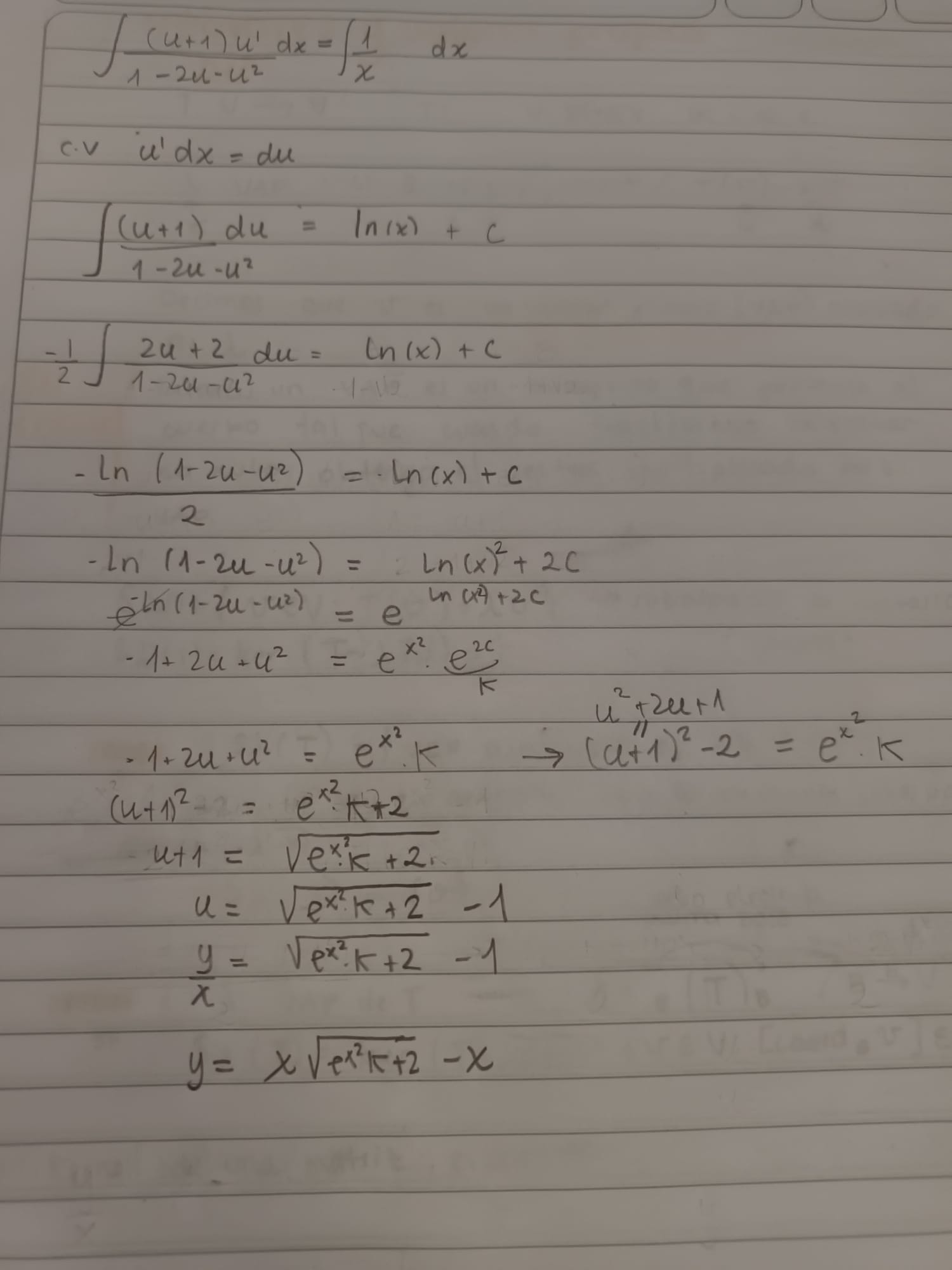
Hola Lucía, gracias por tu respuesta.
Cuidado con las cancelaciones exponente-logaritmo y lo que realizas con el signo de menos delante del primer logaritmo... Te aporto un poco más del procedimiento:
Te invito a que continúes el ejercicio, vas por buen camino a la resolución.
Quedo atento a tu respuesta.
Saludos,
M