Gracias Pablo por le respuesta. Yo diría que lo clave del paso inductivo es que en un tablero de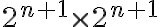 
se puede descomponer en 
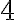tableros de 
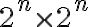. Al probar el paso inductivo, la casilla omitida en el tablero de 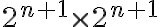cae en uno de los 4 subtableros de 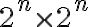y ahí sabes que lo puedes cubrir por la hipótesis de inducción. A los otros 3 conviene pensarlos privados de una casilla al centro y aplicar la hipótesis de inducción. Por último, las 3 casillas que omitiste al centro forman una L y se tapan con una pieza más.
Me parerce importantísimo que comprendan que no sirve como prueba el saber que la cantidad de casillas libres es un múltiplo de 3. Ciertamente eso pasa y es, por ejemplo, consecuencia de lo que se pide probar. Pero el problema es geométrico, no de conteo. Las L son rígidas y tienen un ángulo... si ustedes consideran por ejemplo 3 casillas en línea (que es una cantidad múltiplo de 3), es imposible cubrirlas con una L. Ese contrajemplo muestra que cualquier prueba que no haga intervenir que las dimensiones del tablero son una potencia de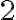
es para sospechar.
Quiero además hacerles notar una asimetría interesante en el uso de la hipótesis de inducción para probar la tesis de inducción: Mientas en un subtablero se usa con toda generalidad, porque no tenemos control sobre cuál es la casilla omitida; en los otros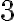
las casillas omitidas las elige quien hace la prueba. Son un elemento nuevo que se introduce a los efectos de hacer la prueba y que no está explícito en el enunciado. Muchas veces al resolver un problema de matemática se precisa imaginar elementos que no están explícitamente mencionados en el enunciado. Es como si están en una habitación tratando de alcanzar algo alto y de pronto se les ocurre salir de la habitación a buscar una escalera porque intuyen que si la tuvieran, llegarían a donde quieren.
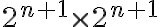se puede descomponer en 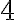tableros de 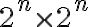. Al probar el paso inductivo, la casilla omitida en el tablero de 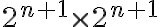cae en uno de los 4 subtableros de 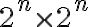y ahí sabes que lo puedes cubrir por la hipótesis de inducción. A los otros 3 conviene pensarlos privados de una casilla al centro y aplicar la hipótesis de inducción. Por último, las 3 casillas que omitiste al centro forman una L y se tapan con una pieza más.Me parerce importantísimo que comprendan que no sirve como prueba el saber que la cantidad de casillas libres es un múltiplo de 3. Ciertamente eso pasa y es, por ejemplo, consecuencia de lo que se pide probar. Pero el problema es geométrico, no de conteo. Las L son rígidas y tienen un ángulo... si ustedes consideran por ejemplo 3 casillas en línea (que es una cantidad múltiplo de 3), es imposible cubrirlas con una L. Ese contrajemplo muestra que cualquier prueba que no haga intervenir que las dimensiones del tablero son una potencia de
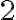es para sospechar. Quiero además hacerles notar una asimetría interesante en el uso de la hipótesis de inducción para probar la tesis de inducción: Mientas en un subtablero se usa con toda generalidad, porque no tenemos control sobre cuál es la casilla omitida; en los otros
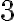las casillas omitidas las elige quien hace la prueba. Son un elemento nuevo que se introduce a los efectos de hacer la prueba y que no está explícito en el enunciado. Muchas veces al resolver un problema de matemática se precisa imaginar elementos que no están explícitamente mencionados en el enunciado. Es como si están en una habitación tratando de alcanzar algo alto y de pronto se les ocurre salir de la habitación a buscar una escalera porque intuyen que si la tuvieran, llegarían a donde quieren.Por cierto, ése y el ejercicio 5 --por otras consideraciones-- son dos de los más didácticos del práctico. Mi calurosa recomendación es que escriban en español la prueba, sin temor de no usar ninguna fórmula ni cálculo. Lo lindo de ese ejercicio es que está despojado de todo mecanismo de manipulación simbólica que permita "tropezarse" con una prueba haciendo cuentas. Al estar despojado de cualquier manipulación simbólica permite verificar que entienden la estructura del razonamiento.
¡Buen trabajo!