Hola,
cuando hoy vimos el "Método de las mallas", quedó planteada la simetría o no de la matriz que relaciona tensiones y corrientes. Consideremos en primer lugar que solamente hay resistencias. Si todas las ecuaciones de malla se plantean de forma tal que "el sentido de recorrido de la malla" coincide con "el sentido de la corriente de malla", entonces los elementos de la diagonal siempre van a quedar positivos y van a coincidir con la suma total de las resistencias de la malla. Los elementos fuera de la diagonal, por ejemplo el lugar ij, contrndrá, a menos de un signo, la suma de las resistencias comunces a las malla i y j. Si solamente hay resistencias, entonces la matriz queda simétrica, ya que el lugar ij y el ji contendrán lo mismo (lo común a ambas mallas). Por ejemlo, podemos ver este circuito, que está en las diapositivas.
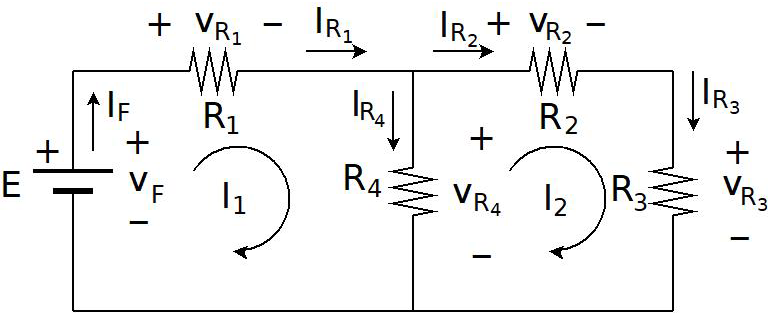
al que le corresponde la ecuación:
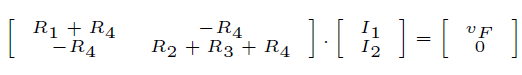
¿Cómo puede romperse la simetría?
Tiene que haber un elemento que provoque una caída en una malla, que dependa de la corriente en otra malla. Por ejemplo, consideren el circuito anterior, pero sustituyan la resistencia R3 por una fuente de tensión dependiente, de valor v_dep=R.I1, es decir, la caída depende de la corriente que entrega la fuente de tensión E. SI plantean las cuentas, verán que el elemento 12 de la matriz no cambia (la malla 1 sigue igual), pero sí cambia el lugar 21!!!
Cualquier cosa, lo trabajamos el lunes próximo. Recuerden que hoy quedó abierto el primer cuestionario. La semana próxima arrancamos con el Principio de Superposición y los Teoremas de Thévenin, Norton y Tellegen.
Saludos cordiales,
Pablo
