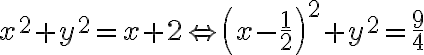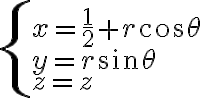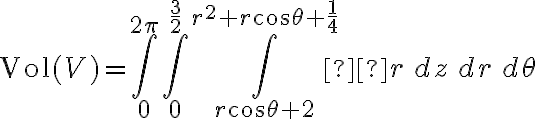Hola. En este caso lo mejor es hacer un cambio de variables a cilíndricas pero tomando un cilindro cuyo eje principal no es el eje  (es decir, el cambio de variable más útil no es
(es decir, el cambio de variable más útil no es 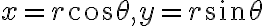 ).
).
Fijate que te están pidiendo el volumen de un sólido que es la intersección del interior del paraboloide 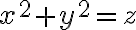 con una de las dos secciones en las que el plano
con una de las dos secciones en las que el plano 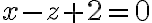 divide a
divide a 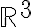 . Gráficamente esos conjuntos se ven como en esta figura: https://www.geogebra.org/m/xg85ddny
. Gráficamente esos conjuntos se ven como en esta figura: https://www.geogebra.org/m/xg85ddny
Fijate que, en el plano 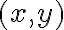 el conjunto donde se intersectan es una circunferencia que no está centrada en el origen. Para ver exactamente cuál es, observá que donde se intersectan se tiene que cumplir que
el conjunto donde se intersectan es una circunferencia que no está centrada en el origen. Para ver exactamente cuál es, observá que donde se intersectan se tiene que cumplir que  y que
y que 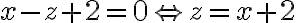 . Entonces las coordenadas
. Entonces las coordenadas  e
e  de los puntos que estén en esa intersección tienen que cumplir:
de los puntos que estén en esa intersección tienen que cumplir:
En el plano 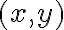 eso se corresponde a la ecuación de una circunferencia de centro
eso se corresponde a la ecuación de una circunferencia de centro 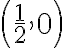 y radio
y radio 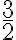 . El sólido que querés calcular corresponde a los puntos cuyas coordenadas
. El sólido que querés calcular corresponde a los puntos cuyas coordenadas  e
e  están en el interior de esa circunferencia, y la coordenada
están en el interior de esa circunferencia, y la coordenada  varía entre el paraboloide
varía entre el paraboloide 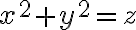 y el plano
y el plano 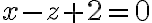 .
.
Así, el cambio de variable más útil en este caso es el que te permite recorrer la circunferencia de centro 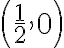 y radio
y radio 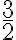 , es decir:
, es decir:
Con ese cambio de variable, se puede ver que la condición 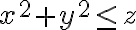 se transforma en
se transforma en 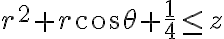 , y la condición
, y la condición 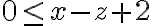 en
en 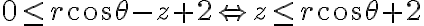 . Como el cambio jacobiano de ese cambio de variable es
. Como el cambio jacobiano de ese cambio de variable es  , el volumen a calcular es:
, el volumen a calcular es:
Calculando esa integral triple llegás a la respuesta correcta.
Saludos