Foro de consultas generales

El circuito te va a quedar algo asi:

--- -| |+ ----R---- +| |- ---

Entonces, por la ley de mallas tenemos que:

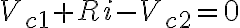$\displaystyle V_{c1} + Ri - V_{c2} = 0$ ( no estaria mal confirmar esto )

$\displaystyle \frac{Q}{C} + R \frac{dQ}{dt} - \frac{Q_0 - Q}{C}=0$

$\displaystyle \frac{Q}{C} + R \frac{dQ}{dt} + \frac{Q}{C}=\frac{Q_0}{C}$

$\displaystyle 2\frac{Q}{C} + R \frac{dQ}{dt}=\frac{Q_0}{C}$

Esto es una ecuación diferencial.

Homogénea

$\displaystyle 2\frac{Q}{C}+R\frac{dQ}{dt} = 0$

Entonces, reordenando:

$\displaystyle 2\frac{Q}{C}= -R\frac{dQ}{dt}$

$\displaystyle -2\frac{R}{C}dt =\frac{dQ}{Q}$

$\displaystyle -2\frac{R}{C}t + \mathbb{C}= \ln(Q)$

y asi la homogenea queda:

$\displaystyle Q = ke^{-2\frac{R}{C}t}$.

Si consideramos como ecuacion particular:

$\displaystyle Q = \frac{Q_0}{2}$

Vemos que funciona ya que efectivamente:

$\displaystyle 2\frac{\frac{Q_0}{2}}{C}+R\frac{d(\frac{Q_0}{2})}{dt}=\frac{Q_0}{C}$

Asi, tenemos que:

$\displaystyle Q(t) = ke^{-2\frac{R}{C}t} + \frac{Q_0}{2}$.

Condiciones iniciales

Para el capacitor cargado inicialmente se tiene que:

$\displaystyle Q(0) = Q_0$

Entonces:

$\displaystyle Q(0) = k + \frac{Q_0}{2} = Q_0$

$\displaystyle k = \frac{Q_0}{2}$

Y asi:

$\displaystyle Q(t) = \frac{Q_0}{2}e^{-2\frac{R}{C}t} + \frac{Q_0}{2} = \frac{Q_0}{2} (1+e^{-2\frac{R}{C}t})$

Para el capacitor descargado inicialmente se tiene que:

$\displaystyle Q(0) = 0$

Entonces:

$\displaystyle Q(0) = k + \frac{Q_0}{2} = 0$

$\displaystyle k = - \frac{Q_0}{2}$

Y asi:

$\displaystyle Q(t) = -\frac{Q_0}{2}e^{-2\frac{R}{C}t} + \frac{Q_0}{2} = \frac{Q_0}{2} (1-e^{-2\frac{R}{C}t})$

Lo hice solo y es como la primer ecuacion diferencial que resuelvo en los ultimos tres años asi que atenti!!