Buenos días. Tenía una consulta del ejercicio 3 del examen de febrero de 2024. Si tuviera que un curso C1 se superpone con un curso C2, y también se superpone con C3, pero C2 y C3 no se superponen entre sí (por ejemplo si C1 es de 1 a 5, C2 de 1 a 2, y C3 de 4 a 5), no sería imposible formar las particiones? Necesito que C1 esté en una partición con C2, también que C1 esté en una partición con C3, pero no puedo tener a C1 en dos particiones diferentes. Tampoco podría tener a C1,C2 y C3 en una misma partición porque C2 y C3 no se superponen entre sí. En este caso sí hay una asignación posible para un estudiante que solicite cursar estos tres cursos: {C1} o {C2,C3} pero no encuentro la forma en la que tendría que construir las particiones.
Desde ya muchas gracias. Saludos.
En respuesta a Anaclara Martha Sigales Pajón
Re: Examen Febrero 2024 - Ejercicio 3
de Fernando Fernandez -
Hola Anaclara.
Lo que decís es correcto, y por eso mismo ese conjunto de cursos no es una instancia válida del problema.
Según la letra se conoce una partición que cumple con las condiciones mencionadas, y, por lo tanto, esa partición tiene que existir. Lo que dice la letra es que esa partición es conocida, es parte de la instancia.
Lo que decís es correcto, y por eso mismo ese conjunto de cursos no es una instancia válida del problema.
Según la letra se conoce una partición que cumple con las condiciones mencionadas, y, por lo tanto, esa partición tiene que existir. Lo que dice la letra es que esa partición es conocida, es parte de la instancia.
En respuesta a Fernando Fernandez
Re: Examen Febrero 2024 - Ejercicio 3
Buenas tardes,
A mi también me generaron dudas las particiones. Yo supuse que existían un número x de particiones S1...Sx tales que cada una tiene cursos que se superponen. Y el grafo me quedó con vértices e1...en conectados a los S1...Sx mediante aristas de valor 1, de esta forma se garantiza que un estudiante solo estará asignado a un curso de cada partición y por tanto se cumple la condición de que no se le asigne un curso que se superponga en horario con otro.
Para completar el grafo cada nodo S1...Sx correspondiente a una partición de S se conecta a los cursos con aristas de peso 1, de forma que nodo Sj tenga una arista con Ci si Ci pertenece al conjunto Sj (i entre 1 y max cursos, j entre 1 y x).
Por último cada curso se une al nodo sumidero t con una arista de valor qi correspondiente al cupo. Y el nodo fuente se une a los estudiantes con una arista de valor pei correspondiente al máximo de cursos a los que se puede anotar cada estudiante.
Leyendo la solución no me quedó claro si es correcto mi razonamiento o está mal asumir particiones diferentes.
Muchas gracias!
saludos,
Romina
A mi también me generaron dudas las particiones. Yo supuse que existían un número x de particiones S1...Sx tales que cada una tiene cursos que se superponen. Y el grafo me quedó con vértices e1...en conectados a los S1...Sx mediante aristas de valor 1, de esta forma se garantiza que un estudiante solo estará asignado a un curso de cada partición y por tanto se cumple la condición de que no se le asigne un curso que se superponga en horario con otro.
Para completar el grafo cada nodo S1...Sx correspondiente a una partición de S se conecta a los cursos con aristas de peso 1, de forma que nodo Sj tenga una arista con Ci si Ci pertenece al conjunto Sj (i entre 1 y max cursos, j entre 1 y x).
Por último cada curso se une al nodo sumidero t con una arista de valor qi correspondiente al cupo. Y el nodo fuente se une a los estudiantes con una arista de valor pei correspondiente al máximo de cursos a los que se puede anotar cada estudiante.
Leyendo la solución no me quedó claro si es correcto mi razonamiento o está mal asumir particiones diferentes.
Muchas gracias!
saludos,
Romina
En respuesta a Romina Hoffman Giorello
Re: Examen Febrero 2024 - Ejercicio 3
de Fernando Fernandez -
Hola Romina.
Noto un par de problemas. El primero tal vez se deba a que te faltó aclarar algo que sí estabas pensando, y el segundo es donde me parece que tu solución no es correcta.
Con respeto a lo primero. A la arista que une al estudiante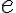 con el subconjunto
con el subconjunto  le das capacidad 1 para evitar asignar un estudiante a dos cursos que se superponen. Eso está bien. El problema ahí es que, tal como lo redactaste, hay una arista entre cada
le das capacidad 1 para evitar asignar un estudiante a dos cursos que se superponen. Eso está bien. El problema ahí es que, tal como lo redactaste, hay una arista entre cada 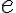 y cada
y cada  , aunque el estudiante no solicite cursar ninguno de los cursos pertenecientes a
, aunque el estudiante no solicite cursar ninguno de los cursos pertenecientes a  . Entonces, al aplicar Ford Fulkerson se podría terminar asignando
. Entonces, al aplicar Ford Fulkerson se podría terminar asignando 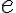 a un curso que no solicitó. Te estaría faltando agregar que hay una arista entre
a un curso que no solicitó. Te estaría faltando agregar que hay una arista entre 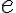 y
y  si y solo si
si y solo si 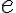 solicita cursar algún curso perteneciente a
solicita cursar algún curso perteneciente a  (en la solución esto se dice con
(en la solución esto se dice con 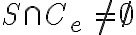 ). ¿Puede ser que te haya faltado aclararlo?
). ¿Puede ser que te haya faltado aclararlo?
El segundo problema tiene que ver con las aristas entre los subconjuntos y los cursos. Ahí lo redactaste bien, no hay una arista entre cada subconjunto y cada curso
y cada curso  , sino solo entre aquellos
, sino solo entre aquellos  y
y  tales que
tales que  pertenece a
pertenece a  . De esta forma te asegurás que ningún estudiante sea asignado a un curso que no solicitó.
. De esta forma te asegurás que ningún estudiante sea asignado a un curso que no solicitó.
El problema es que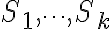 es una partición del conjunto de cursos
es una partición del conjunto de cursos 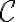 , por lo que cada curso
, por lo que cada curso  pertenece a exactamente un subconjunto. Como consecuencia,
pertenece a exactamente un subconjunto. Como consecuencia,  tendría solo una arista entrante, por lo cual el máximo de estudiantes que se le puede asignar es 1 (en lugar de
tendría solo una arista entrante, por lo cual el máximo de estudiantes que se le puede asignar es 1 (en lugar de 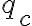 , su cantidad máxima).
, su cantidad máxima).
Creo que el problema está en que le estás llamando partición a los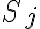 . Hay una única partición de
. Hay una única partición de 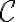 , llamada
, llamada  en la letra, y los
en la letra, y los 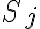 , elementos de
, elementos de  , son subconjuntos de
, son subconjuntos de 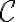 .
.
¿Esto te parece correcto?
Noto un par de problemas. El primero tal vez se deba a que te faltó aclarar algo que sí estabas pensando, y el segundo es donde me parece que tu solución no es correcta.
Con respeto a lo primero. A la arista que une al estudiante
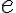 con el subconjunto
con el subconjunto  le das capacidad 1 para evitar asignar un estudiante a dos cursos que se superponen. Eso está bien. El problema ahí es que, tal como lo redactaste, hay una arista entre cada
le das capacidad 1 para evitar asignar un estudiante a dos cursos que se superponen. Eso está bien. El problema ahí es que, tal como lo redactaste, hay una arista entre cada 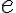 y cada
y cada  , aunque el estudiante no solicite cursar ninguno de los cursos pertenecientes a
, aunque el estudiante no solicite cursar ninguno de los cursos pertenecientes a  . Entonces, al aplicar Ford Fulkerson se podría terminar asignando
. Entonces, al aplicar Ford Fulkerson se podría terminar asignando 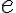 a un curso que no solicitó. Te estaría faltando agregar que hay una arista entre
a un curso que no solicitó. Te estaría faltando agregar que hay una arista entre 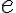 y
y  si y solo si
si y solo si 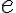 solicita cursar algún curso perteneciente a
solicita cursar algún curso perteneciente a  (en la solución esto se dice con
(en la solución esto se dice con 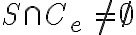 ). ¿Puede ser que te haya faltado aclararlo?
). ¿Puede ser que te haya faltado aclararlo?El segundo problema tiene que ver con las aristas entre los subconjuntos y los cursos. Ahí lo redactaste bien, no hay una arista entre cada subconjunto
 y cada curso
y cada curso  , sino solo entre aquellos
, sino solo entre aquellos  y
y  tales que
tales que  pertenece a
pertenece a  . De esta forma te asegurás que ningún estudiante sea asignado a un curso que no solicitó.
. De esta forma te asegurás que ningún estudiante sea asignado a un curso que no solicitó. El problema es que
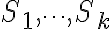 es una partición del conjunto de cursos
es una partición del conjunto de cursos 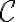 , por lo que cada curso
, por lo que cada curso  pertenece a exactamente un subconjunto. Como consecuencia,
pertenece a exactamente un subconjunto. Como consecuencia,  tendría solo una arista entrante, por lo cual el máximo de estudiantes que se le puede asignar es 1 (en lugar de
tendría solo una arista entrante, por lo cual el máximo de estudiantes que se le puede asignar es 1 (en lugar de 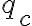 , su cantidad máxima).
, su cantidad máxima). Creo que el problema está en que le estás llamando partición a los
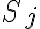 . Hay una única partición de
. Hay una única partición de 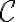 , llamada
, llamada  en la letra, y los
en la letra, y los 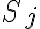 , elementos de
, elementos de  , son subconjuntos de
, son subconjuntos de 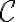 .
. ¿Esto te parece correcto?
En respuesta a Fernando Fernandez
Re: Examen Febrero 2024 - Ejercicio 3
Buenas tardes Fernando,
Muchas gracias por tu respuesta tan detallada!.
De lo primero si me había olvidado de mencionarlo pero lo tuve en cuenta. Había interpretado mal la partición S de C, como que era un único conjunto de cursos que se superponen entre ellos. Por lo que entendí con tu respuesta la partición S está compuesta por subconjuntos de C que representan los subconjuntos de cursos que se superponen entre ellos. Por ejemplo S= {(c1,c2,c3), (c4,c5)} implica que los cursos {c1,c2,c3} se superponen en el tiempo, y también c4 se superpone con c5.
Con esta interpretación W= E x S sería de la forma: {(e_1, (c1,c2,c3)), (e_1,(c4,c5)),...(e_n,(c1.c2,c3)),(e_n,(c4,c5))}.
Muchas gracias!
saludos
Muchas gracias por tu respuesta tan detallada!.
De lo primero si me había olvidado de mencionarlo pero lo tuve en cuenta. Había interpretado mal la partición S de C, como que era un único conjunto de cursos que se superponen entre ellos. Por lo que entendí con tu respuesta la partición S está compuesta por subconjuntos de C que representan los subconjuntos de cursos que se superponen entre ellos. Por ejemplo S= {(c1,c2,c3), (c4,c5)} implica que los cursos {c1,c2,c3} se superponen en el tiempo, y también c4 se superpone con c5.
Con esta interpretación W= E x S sería de la forma: {(e_1, (c1,c2,c3)), (e_1,(c4,c5)),...(e_n,(c1.c2,c3)),(e_n,(c4,c5))}.
Muchas gracias!
saludos
