Es cierta la siguiente proposición:
Si yo sé cuántos vértices de grado 0, cuántos de grado 1, cuántos de grado 2, y así para todo n natural, esto me determina un único grafo simple (Ignorando que existen isomorfismos de éste).
Ejemplo:
Si yo se que un grafo G tiene
0 vértices de grado 0
1 vértice de grado 1
2 vértices de grado 2
1 vértice de grado 3
y 0 vértices de grado mayor a 3
hay solo un grafo simple posible que cumpla esta definición (y sus isomorfismos).
Buenas, Alan.
No, no es cierta. Podés pensar un contraejemplo con seis vértices.
Como dato, la forma que tenemos en matemática de decir eso que dijiste es "a menos de isomorfismo". O sea, tu pregunta sería: Dados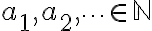
, ¿existe un único grafo, a menos de isomorfismo, que tenga 
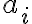vértices de grado 
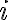, para todo ?
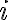Saludos.
No, no es cierta. Podés pensar un contraejemplo con seis vértices.
Como dato, la forma que tenemos en matemática de decir eso que dijiste es "a menos de isomorfismo". O sea, tu pregunta sería: Dados
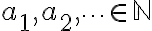, ¿existe un único grafo, a menos de isomorfismo, que tenga 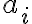vértices de grado 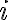, para todo 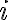?Saludos.
En Matemática aparecen en varias áreas (*) unos grafos que se llaman Dynkin Graphs.
Compará D_6 con E_6, o D_7 con E_7 o bien D_8 con E_8.
Estaría bueno que pruebes que, por ejemplo, D_6 y E_6, no son isomorfos, aunque tienen la misma cantidad de vértices, con los mismos grados.
Saludos
Marcelo Lanzilotta
(*) Ver en: https://www.ams.org/journals/notices/199705/reiten.pdf