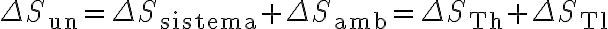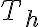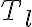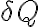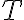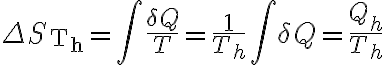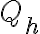Hola Victoria, buenas tardes.
Hay un error en el razonamiento con respecto a la entropía. Vayamos por lo primero.
Los cálculos que intervienen en la segunda ley (al igual que ocurre en la primera) dependen de cómo se definió la frontera del sistema (superficie ficticia que separa el sistema del ambiente). Consideremos que definimos esta frontera de manera que es una superficie que deja dentro el dispositivo que trabaja en un ciclo (en este caso, la máquina térmica), y que el ambiente quedará definido entonces por todo lo demás, es decir, las dos reservas térmicas. Por una cuestión técnica permitime definir esta frontera como una que "roza" las reservas térmicas (ahora ahondo en esto).
Con eta definición, rápidamente se puede calcular la variación de entropía del universo como (considerando que la máquina térmica trabaja en un ciclo):
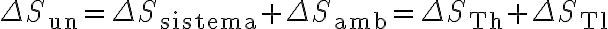
siendo
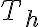
la fuente de alta y
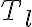
la fuente de baja temperatura. Cuando realizamos el cálculo de la entropía necesitamos saber dos cosas: el calor que se transfiere (cuantificado como
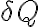
en la definición de entropía) y la temperatura a la cual se da dicha transferencia de calor (que se refleja en el denominador de la definición de entropía, como la temperatura
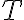
).
Calculemos la variación de entropía de la fuente de alta. Dado que sabemos la temperatura a la cual se transfiere calor desde la reserva hacia el sistema (que dicha es temperatura es
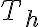
constante, y lo sabemos porque definimos la frontera "rozando" la fuente) la variación de entropía de dicha reserva térmica es:
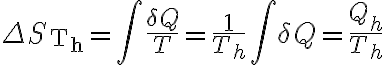
En este ciclo, el sistema toma calor de la fuente de alta en dos procesos, intercambiando calor a una temperatura
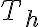
constante (vista desde la fuente). Es cierto lo que mencionás acerca de que el gas varía su temperatura, pero el cálculo, en este caso puntual de esta reserva, ve la transferencia de calor desde el lado de la misma. ¿Cuánto calor intercambia la reserva? Es decir, ¿cuánto vale
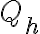
? Eso fue determinado previamente en función del gas. Por ejemplo, el gas absorbió calor en los procesos 2-3 y 3-4 de la fuente de alta, en una cantidad igual y opuesta a la que liberó la fuente de alta al gas.
El razonamiento es análogo con la fuente de baja temperatura, pero intercambiando calor con el sistema a una temperatura
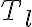
debido a cómo definimos la frontera del sistema.
Saludos,
m
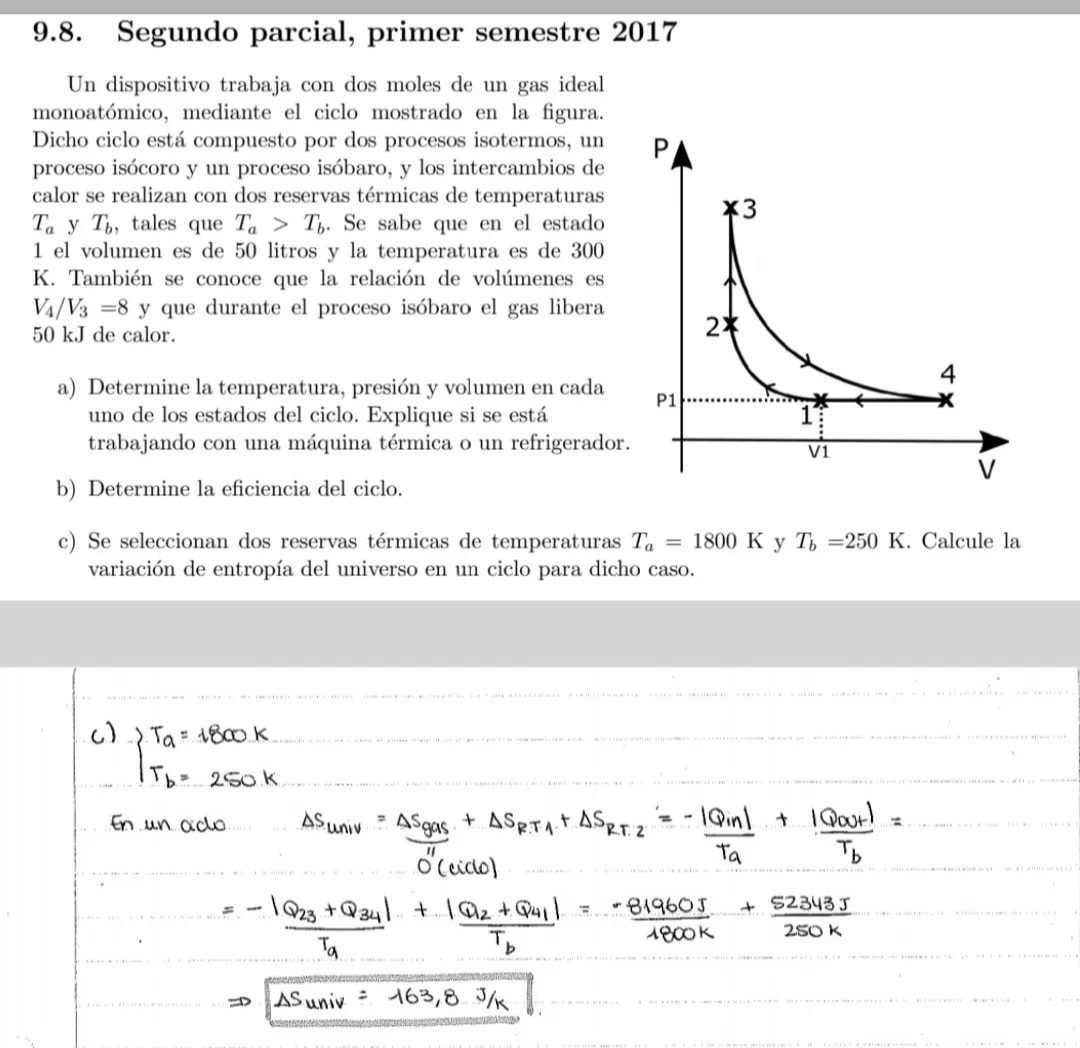 buenas, viendo la solución de este parcial, no entiendo por qué para calcular la variacion de entropía del universo divide Q sobre T, siendo que eso solo puede hacerse en procesos a T constante, y en los procesos 23 y 41 T no es constante. Ademas utiliza los calores calculados en la parte anterior del ejercicio, donde las temperaturas eran otras.
buenas, viendo la solución de este parcial, no entiendo por qué para calcular la variacion de entropía del universo divide Q sobre T, siendo que eso solo puede hacerse en procesos a T constante, y en los procesos 23 y 41 T no es constante. Ademas utiliza los calores calculados en la parte anterior del ejercicio, donde las temperaturas eran otras.