Buenas! Espero se encuentren bien.
El ejercicio es el siguiente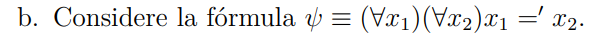



Para este ejercicio y en general, si me piden probar que un conjunto no es consistente maximal lo único que se me ocurre es encontrar una formula phi tal que existe un M1:eta que modela a { psi } que modela phi y un M2:eta que modela a { psi } que no modela phi.
Entonces existen M que modelan { psi } pero que no modelan ni phi ni su negación.
Tanto M1 como M2 pertenecen a Mod({ psi }), pero ni phi ni not phi pertenecen a Th(Mod({ psi })) ya que existen modelos que no las modelan y deberían ser modeladas por todos los modelos para pertenecer.
Como Th(Mod({ psi })) = Cons({ psi }) entonces ni phi ni su negación pertenecen a Cons({ psi }), entonces por propiedades de consistente maximal, Cons({ psi }) no puede serlo.
Como testigo de esta demostración utilicé (Paratodo x)P(x), seguí estos pasos con esa formula.
1. Este razonamiento es correcto?
2. Existe otra forma, mas simple o no, de probar esto?
Revise otras caracterizaciones de consistente maximal pero no se me ocurrió como utilizarlas en este caso.
Muchas gracias!
Saludos,
Diego Furrer.
