Buenas! Espero se encuentren bien.
El ejercicio es el siguiente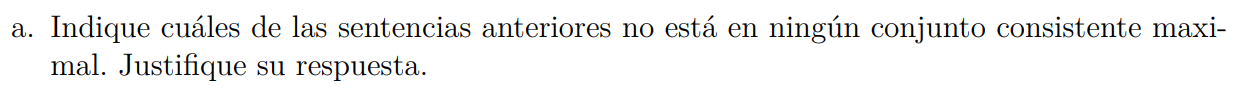
Quiero probar que la siguiente formula no pertenece a ningun consistente maximal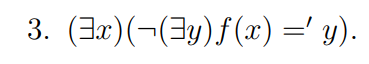
Intuitivamente es obvio que es siempre falsa ya que las funciones son completas, entonces para cada x del universo me tiene que devolver un elemento del universo.
Mi idea para resolver esto fue medio rara. Lo que hice fue probar que la derivación de la negación de la formula se puede lograr sin ninguna hipótesis.
Entonces, por correctitud, la negación de la formula es lógicamente válida, entonces la formula es una contradicción.
Entonces no existe consistente maximal que contenga esta formula ya que si esto ocurriera, entonces al contener una contradicción podría derivar bottom y por ende no sería consistente.
Mi pregunta 1 es: Es esta forma de demostrarlo válida?
A su vez, la forma de trabajar con una función f(x) genérica semánticamente para mantener un Modelo genérico me deja dudas.
Como probé con un modelo genérico que la frase es falsa, entonces es falsa para todo modelo, entonces es una contradicción, entonces no puede estar en un consistente maximal ya que si estuviera podría derivar bottom.
Mi pregunta 2 es: Es esto correcto? Especialmente la parte en la que paso de f(x) a F(x)
Mi pregunta 3 es: Podría haber probado semánticamente que la negación de la formula es lógicamente válida? Y con eso asumir que la formula entonces es contradicción y después los mismos pasos que arriba?
Muchas gracias!
Saludos,
Diego Furrer.
