Consultas de pruebas anteriores

Buenas

Intentemos analizar la información que brinda el ejercicio.

El punto I, dice que las pendientes de las rectas tangentes de $f$ en a y de $g$ en $a + 1$ son paralelas. Es decir $f^{\prime}(x) = g^{\prime}(x + 1)$

En particular si llamamos $h(x) = g(x + 1)$ tenemos que $h^{\prime}(x) = f^{\prime}(x)$

Dos funciones con igual derivada difieren en una constante, podemos decir que $h(x) = f(x) + k$.

Para conocer la constante 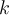$k$ vamos a la informacion (III).

$\displaystyle \int_{0}^{2} g(x) dx = \int_{-1}^{1} h(x) dx$

aqui solo realice un cambio de variable lineal

Pero como $h(x) = f(x) + k$ tenemos que

$\displaystyle \int_{-1}^{1} h(x) dx=\int_{-1}^{1} f(x) + k dx = \int_{-1}^{1} f(x) dx + 2k$

Por (III) sabemos que $\displaystyle \int_{-1}^{1} f(x) dx = 2+\int_{0}^{2}g(x) dx = 2+\int_{-1}^{1} h(x)dx = 2+ \int_{-1}^{1} f(x)dx +2k$

Es decir $k = -1$

Podemos concluir entonces que $h(x) = f(x) - 1$

Luego para estudiar el limite en 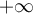$+\infty$ basta ver que si $\displaystyle \lim_{x \to + \infty} f(x) = 0$ entonces $\displaystyle \lim_{x \to + \infty} h(x) = -1$

Por último como $h(x) = g(x+1)$, se tiene que $\displaystyle \lim_{x \to +\infty} h(x) = \lim_{x \to +\infty} g(x) = -1$

Saludos