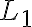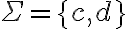TeoLeng: [2017] [Segundo Parcial] [Ejercicio 2]

Hola! Al considerar lenguajes sobre el mismo alfabeto como dice la letra, me surgió la siguiente duda.

Por ejemplo: para la parte a) planteé L1 = {a^k b^k ; k > 0} y L2 = {c^k d^k ; k > 0}, con el alfabeto {a,b,c,d} y al plantear la intersección te queda el vacío, el cual es regular. Pero al tomar en cuenta "lenguajes sobre el mismo alfabeto", requiere que tengan los mismos símbolos? Es "ilegal" lo que planteé?

Una pregunta más general que nace de esto es: todo alfabeto que contenga a los símoblos del lenguaje y más es un alfabeto para el lenguaje?

Gracias!

Re: [2017] [Segundo Parcial] [Ejercicio 2]

de Santiago Gongora - viernes, 5 de julio de 2024, 15:27

Hola Nicolás ¿cómo estás?

Es una pregunta re interesante la que hacés porque tiene dos respuestas dependiendo de cómo se analice el problema.

En un plano conceptual eso sería perfectamente válido, porque $\Sigma$ es un conjunto de símbolos cualquiera. El lenguaje que use ese alfabeto tiene que cumplir que sus tiras tienen que ser una secuencia (ordenada) de esos símbolos. Así que, hasta ahí, todo bien.

El tema es que, con esa definición de alfabeto, se podría decir que cualquier lenguaje comparte alfabeto con cualquier otro: basta con tomarse un conjunto enorme de símbolos y listo. Así que en el plano de la evaluación, esa aclaración que decís se incluye para hacer referencia a que el alfabeto $\Sigma$ de un lenguaje se puede definir como "el conjunto mínimo necesario para construir las tiras del lenguaje". Por lo tanto, bajo esa óptica, para tu $L_1$ el alfabeto es $\Sigma = \{a,b\}$ y para tu $L_2$ el alfabeto es $\Sigma = \{c,d\}$ .

De cualquier forma, para la evaluación lo importante es que esté claro lo que estás razonando y, en este caso, es claro que lo estás haciendo correctamente.

Saludos,
Santi (respuesta avalada por JJ :) )