Hola,
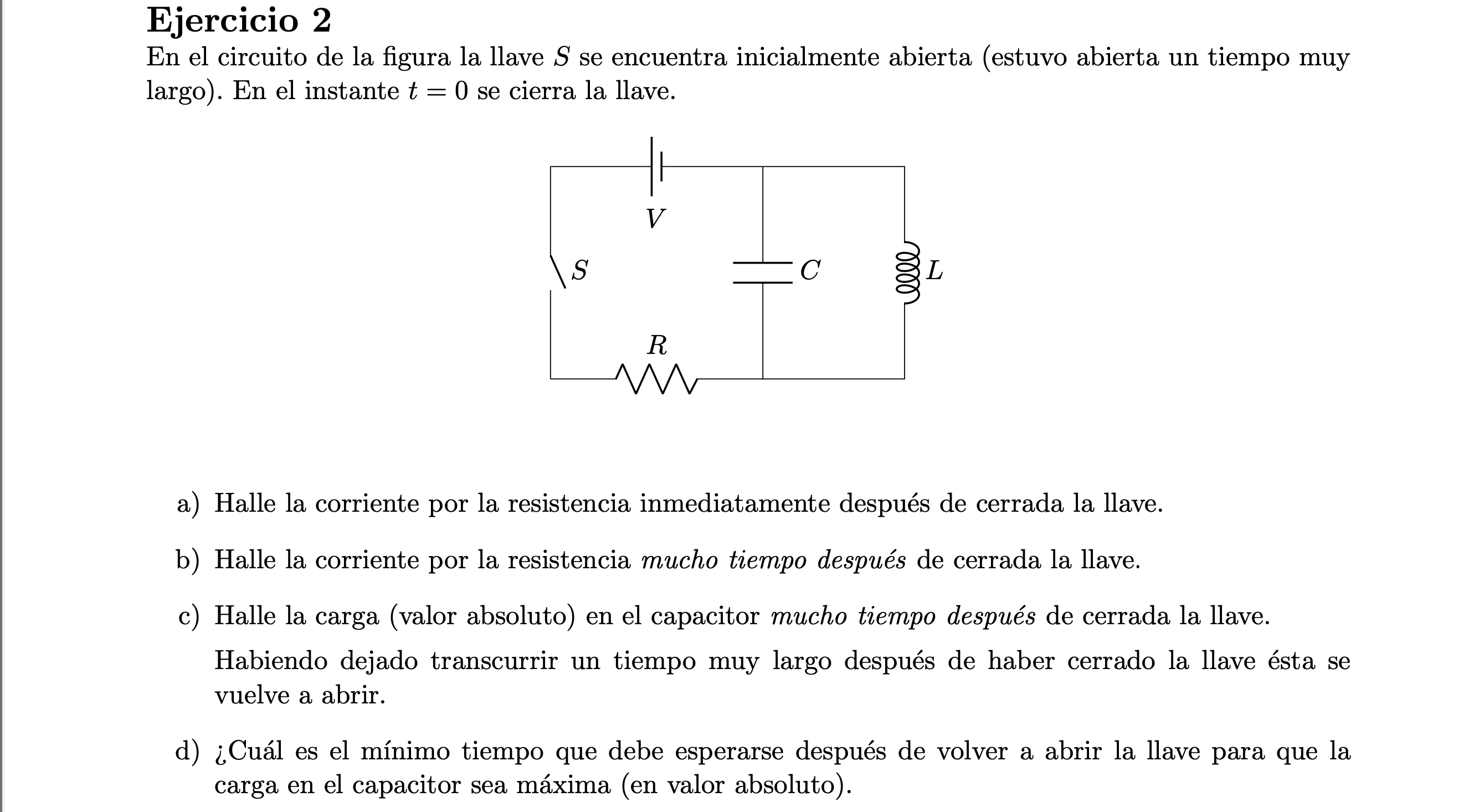
Para ver el desfasaje entre ambos hay que ver lo siguiente, si calculas la carga en función del tiempo vas a encontrar que en el caso del ejercicio cuando se abre la llave nuevamente, la carga en el capacitor es nula por lo tanto la ecuación es de la forma q(t)= CV_L sen(wt), entonces la energía es proporcional a sen²(wt). Ojo que la solución para q(t) puede ser un coseno también porque la solución es de la forma q(t)=Acos(wt)+Bsen(wt) donde A y B se determinan por las condiciones iniciales, es decir cuanta carga había en el capacitor cuando se abrió la llave, etc. La energía en el inductor depende de la intensidad, es decir de la derivada que en este caso es un coseno, por lo tanto están desfasadas las energías. Esto es correcto ya que el circuito LC es oscilatorio y eso lo compruebas resolviendo mallas para el circuito en cuestión.
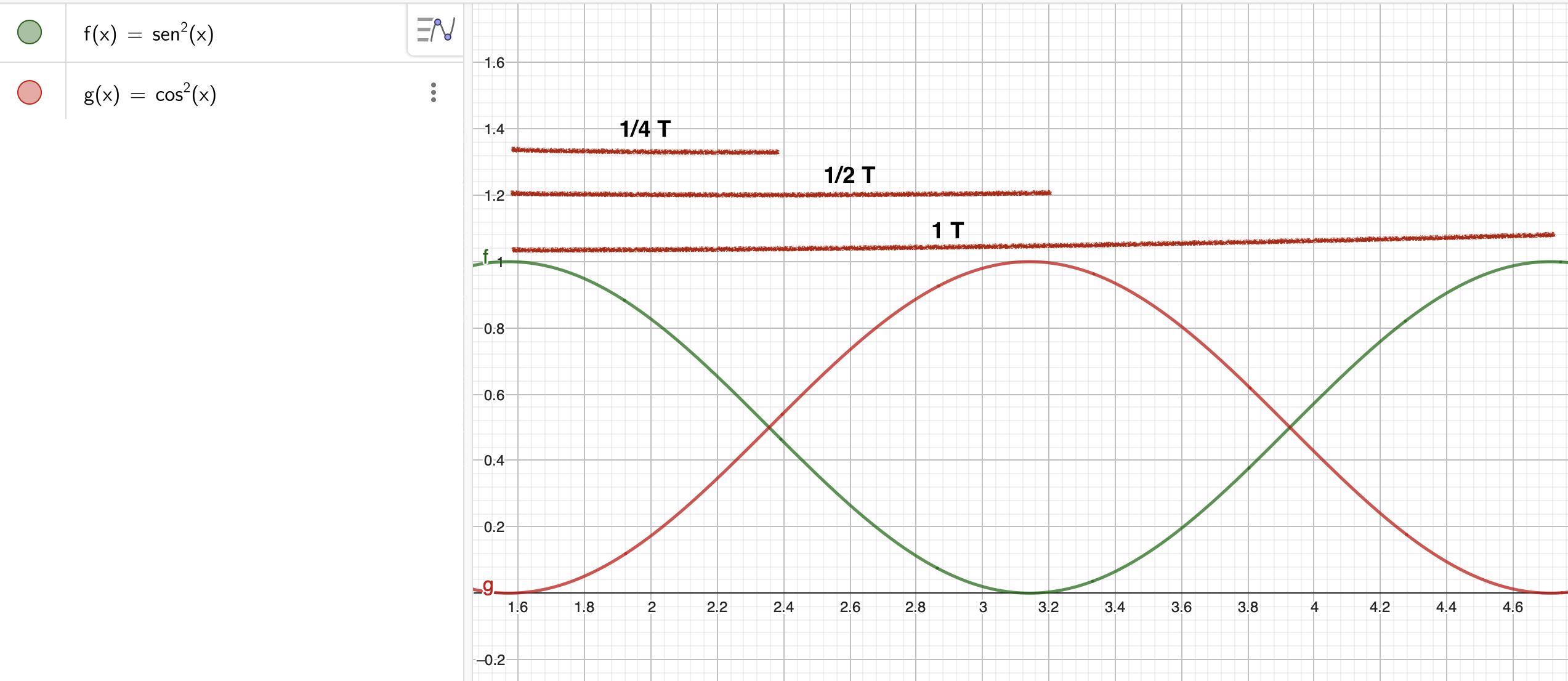
Respecto al gráfico es correcto lo que mencionas, pero se me olvido mencionarte el detalle de que el argumento de las funciones son de la forma wt, es decir que puedo re-escribirlo de la forma (2pi/T)t, y para t=0 la energía en el capacitor es cero y en el inductor es máxima. Pero para cuarto de periodo la energía en el capacitor es máxima pero para el inductor es minima.
Sino me equivoco a la función que me enviaste en la imagen, le faltaría un factor de 2 pi multiplicando en el argumento de las funciones.
Saludos