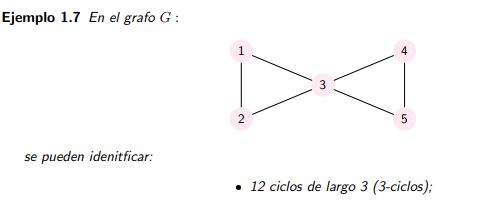
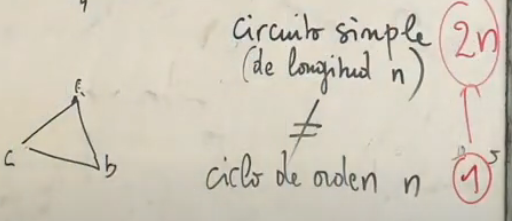Buenas, en el repartido teórico, en la parte de ciclos, se indica en una cierta figura que hay 12 "3-ciclos", la única manera de que se de esto es contando cada ciclo dos veces, o sea que importe el orden. Pero en las clases de Openfing, se explica que por mas que hayan 3 circuitos en un grafo de 3 vértices, solo va a haber 1 3-ciclo. Cual es la definición correcta?
Hola Facundo. No hay una definición correcta sobre como contar la cantidad de ciclos en un grafo. Para ser coherente con la definición de "caminos" como secuencia o sucesión de vértices-aristas del libro Grimaldi, hemos optado por la convención de que dos caminos se consideran iguales si y solo si determinan la misma secuencia de vértices-aristas.
Eso implica que es importante el orden de recorrido de los vértices-aristas.
En el caso del un ciclo importa el vértice inicial (que es el mismo que el vértice final) asi también como el sentido en el que se recorre el ciclo (esta convención es la más común, puede que en alguna edición anterior hayan optado por alguna otra convención sobre el conteo de ciclos por eso escribimos estas notas ).
Saludos,
Claudio
Eso implica que es importante el orden de recorrido de los vértices-aristas.
En el caso del un ciclo importa el vértice inicial (que es el mismo que el vértice final) asi también como el sentido en el que se recorre el ciclo (esta convención es la más común, puede que en alguna edición anterior hayan optado por alguna otra convención sobre el conteo de ciclos por eso escribimos estas notas ).
Saludos,
Claudio
Gracias! Duda despejada
Estimado Facundo:
Lo hemos explicado en cada uno de los 4 teóricos de este curso. Vamos, entonces a aclararlo también en este foro.
1. El texto que usted cita es de ESTE año y los vídeos a los que refiere son de años anteriores. Por ende la respuesta a su pregunta es clara: hay que tomar la definición del texto de este año. O sea, importa el orden y dónde comienza (y termina) el ciclo.
2. Es "incorrecto" lo que afirma el, profesor Miquel en esos vídeos de Opening? Respuesta: NO. Simplemente que en años anteriores se tomaba otra acepción del término ciclo.
AMBAS acepciones son aceptadas en la literatura matemática internacional.
Este año tomamos la definición de ciclo que entiende que un ciclo es un CAMINO con ciertas propiedades (cerrado, de largo mayor o igual a tres, sin repetir vértices excepto el primero = último).
Saludos,
Marcelo Lanzilotta
Lo hemos explicado en cada uno de los 4 teóricos de este curso. Vamos, entonces a aclararlo también en este foro.
1. El texto que usted cita es de ESTE año y los vídeos a los que refiere son de años anteriores. Por ende la respuesta a su pregunta es clara: hay que tomar la definición del texto de este año. O sea, importa el orden y dónde comienza (y termina) el ciclo.
2. Es "incorrecto" lo que afirma el, profesor Miquel en esos vídeos de Opening? Respuesta: NO. Simplemente que en años anteriores se tomaba otra acepción del término ciclo.
AMBAS acepciones son aceptadas en la literatura matemática internacional.
Este año tomamos la definición de ciclo que entiende que un ciclo es un CAMINO con ciertas propiedades (cerrado, de largo mayor o igual a tres, sin repetir vértices excepto el primero = último).
Saludos,
Marcelo Lanzilotta