Hola, tengo una consulta en el cálculo de la potencia del resorte de torsión. Yo traté de aplicar la fórmula de la hoja de fórmulas para calcular la potencia, usando como punto O. Entonces, como la velocidad en O es 0, me queda que esta es igual a M(ext).w. Como quiero calcular el trabajo que hace en el sistema, tome como w la velocidad del sistema, que es según el eje k + la velocidad según el eje de la barra, pero la sugerencia me dice que solo considere la velocidad según k. No me queda claro por qué, si el trabajo en teoría es en el sistema. Lo único que se me ocurrió es que tal vez el sistema no sea un rígido, pero las distancias mutuas se mantienen constantes. 
Hola, Sebastián
Muy buena pregunta.
Vayamos por partes:
- El trabajo del resorte de torsión es sobre la barra (que tiene velocidad angular únicamente según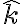
), así que esa es la expresión que debés utilizar.
- El sistema conformado por la barra + la rueda, mantiene la distancia constante entre todo par de puntos, por más que las velocidades angulares de sus partes sean diferentes. Esto sucede efectivamente porque la barra no tiene espesor. Esto hace que parezca posible modelar el objeto como un único rígido. Pero...
Muy buena pregunta.
Vayamos por partes:
- El trabajo del resorte de torsión es sobre la barra (que tiene velocidad angular únicamente según
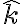), así que esa es la expresión que debés utilizar.- El sistema conformado por la barra + la rueda, mantiene la distancia constante entre todo par de puntos, por más que las velocidades angulares de sus partes sean diferentes. Esto sucede efectivamente porque la barra no tiene espesor. Esto hace que parezca posible modelar el objeto como un único rígido. Pero...
- ¿Porqué no podés considerar a todo el sistema como un único rígido (de velocidad angular según 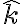y según el eje de la rueda)? Porque en ese caso, la articulación que está en O (cilíndirca de eje fijo y vertical) no puede lograr el movimiento observado (la articulación en O no puede rotar según el eje de la rueda).
Espero se entienda, cualquier cosa repreguntá.
Saludos!
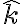y según el eje de la rueda)? Porque en ese caso, la articulación que está en O (cilíndirca de eje fijo y vertical) no puede lograr el movimiento observado (la articulación en O no puede rotar según el eje de la rueda).Espero se entienda, cualquier cosa repreguntá.
Saludos!
Buenas, tengo unas dudas de la parte b de este ejercicio.
¿Por qué en la solución se usa la ecuación de energía cinética en O y además toma en cuenta el momento del resorte de torsión? Eso es válido siendo solamente el aro el sistema de estudio? Y por qué no toma en cuenta el potencial del peso? (o al menos no logro darme cuenta en qué parte está incluido). Por último, cómo es el vínculo entre el aro y la barra? Hay fuerzas reactivas? Porque eso me hizo dudar en un primer momento si la energía se conserva o no.
Muchas gracias.
¿Por qué en la solución se usa la ecuación de energía cinética en O y además toma en cuenta el momento del resorte de torsión? Eso es válido siendo solamente el aro el sistema de estudio? Y por qué no toma en cuenta el potencial del peso? (o al menos no logro darme cuenta en qué parte está incluido). Por último, cómo es el vínculo entre el aro y la barra? Hay fuerzas reactivas? Porque eso me hizo dudar en un primer momento si la energía se conserva o no.
Muchas gracias.
Hola Nara
Varias cosas:
- La barra no tiene energía cinética porque no tiene masa, así que la energía del aro o la del sistema total es equivalente.
- Para estudiar la conservación de la energía mecánica del aro individualmente, tenés que resolver las fuerzas y momentos reactivos en el centro del aro y ver que son conservativos. Es más sencillo considerar el sistema completo, dado que la articulación en O ya la tenés resuelta (Omitiendo el peso, en O es donde se ejercen los momentos y fuerzas externas del sistema completo)
- El punto O, si bien no es parte del aro, si es parte de su expansión rígida. Para ver esto considerá que la distancia de O a cualquier punto del aro permanece constante en el tiempo. Así que O es un punto adecuado para hallar la energía cinética del aro (y por tanto del sistema completo)
- Para hallar la energía cinética de un rígido, es necesario utilizar un punto como referencia (fijate la expresión en la hoja de fórmulas). Ese punto debe pertenecer al rígido (o a su expansión rígida). Por su puesto, el resultado de la energía cinética no dependerá del punto elegido, por lo que es conveniente elegir puntos que simplifiquen las cuentas (centro de masa, puntos fijos, si es que hay, etc.)
- El potencial del peso no aparece en la solución, pero podría. Esto no cambia nada, porque la altura del centro de masas es constante, entonces la energía potencial gravitatoria también lo será. Cuando derives para encontrar la ecuación de movimiento ese término se va.
Espero haber sido claro.
Saludos!
Varias cosas:
- La barra no tiene energía cinética porque no tiene masa, así que la energía del aro o la del sistema total es equivalente.
- Para estudiar la conservación de la energía mecánica del aro individualmente, tenés que resolver las fuerzas y momentos reactivos en el centro del aro y ver que son conservativos. Es más sencillo considerar el sistema completo, dado que la articulación en O ya la tenés resuelta (Omitiendo el peso, en O es donde se ejercen los momentos y fuerzas externas del sistema completo)
- El punto O, si bien no es parte del aro, si es parte de su expansión rígida. Para ver esto considerá que la distancia de O a cualquier punto del aro permanece constante en el tiempo. Así que O es un punto adecuado para hallar la energía cinética del aro (y por tanto del sistema completo)
- Para hallar la energía cinética de un rígido, es necesario utilizar un punto como referencia (fijate la expresión en la hoja de fórmulas). Ese punto debe pertenecer al rígido (o a su expansión rígida). Por su puesto, el resultado de la energía cinética no dependerá del punto elegido, por lo que es conveniente elegir puntos que simplifiquen las cuentas (centro de masa, puntos fijos, si es que hay, etc.)
- El potencial del peso no aparece en la solución, pero podría. Esto no cambia nada, porque la altura del centro de masas es constante, entonces la energía potencial gravitatoria también lo será. Cuando derives para encontrar la ecuación de movimiento ese término se va.
Espero haber sido claro.
Saludos!