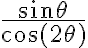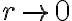Foro de Ejercicios fuera de los Prácticos

f(x,y)=rsin⁡θ(r2)r2(cos⁡2θ−sin⁡2θ)=r3sin⁡θr2cos⁡2θ=rsin⁡θcos⁡2θf(x, y) = \frac{r \sin \theta (r^2)}{r^2 (\cos^2 \theta - \sin^2 \theta)} = \frac{r^3 \sin \theta}{r^2 \cos 2\theta} = \frac{r \sin \theta}{\cos 2\theta}

Entonces, lim⁡r→0rsin⁡θcos⁡2θ=0\lim_{r \to 0} \frac{r \sin \theta}{\cos 2\theta} = 0

Para el caso cuando ∣x∣=∣y∣:

  lim⁡(x,y)→(0,0)f(x,y)=A \lim_{(x,y) \to (0,0)} f(x, y) = A

entonces A debería ser 0