Buenas tardes, dos anuncios:
1. Primero una errata en el último teorema que enuncié sobre caminos Hamiltonianos en mi teórico:
Teorema: Sea G=(V,E) un grafo simple con |V|=n. Si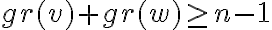 
para todo par de vértices adyacentes distintos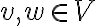 
entonces G admite un camino Hamiltoniano.
O sea con chequear la condición con adyacentes no alcanza, hay que chequearla para todo par de vértices distintos (hay contraejemplos si no).
Hay un criterio análogo (Teorema 11.9 del Grimaldi) que dice que si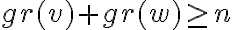 
para todo par de vértices adyacentes entonces G admite un camino Hamiltoniano (observar que esta condición por un lado es un poquito más fuerte que la anterior porque pide que la suma de los grados de vértices sea mayor a n-1 pero por otro lado es más débil en el sentido que no importa que pasa con la suma de los grados de vértices que no sean adyacentes).
2. Este jueves de 11:00 a 12:00 voy a poner una clase de consulta y en caso que no tengan consulta haremos algunos ejemplos más de las cosas vistas en la última clase de teórico. No voy a ver nada nuevo, solo reforzar un poco lo de la última clase con más ejemplos. En cuanto me confirmen el salón se los paso por acá. Si no pueden venir no pasa nada, el jueves 10 también pienso poner otra clase de consulta a las 13:00 para el parcial.
Saludos,
Claudio