Práctico 11 - Foro de consultas

Buenas.

Venís bien encaminado.

Te sugiero que primero calcules 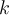$k$, para obtener una expresión de la forma: $n = 2^{a+kb}$. Para esto te conviene tener en cuenta que $3=6 \times 2$, y usar alguno de los datos de la letra.

Una vez que tengas esto, te sugiero usar la Proposición 3.7.8 de las notas del curso. En particular la propiedad del numeral 7, que dice lo siguiente:

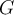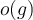Sea $G$ un grupo, y $g \in G$. Si $o(g)$ es finito, entonces: $o(g^m) = \frac{ o(g) }{ mcd( m, o(g) ) }, \quad \forall \ m \in \mathbb{Z} .$

En particular, si tu grupo es cíclico (y finito), y $g$ es un generador, esta expresión te permite hallar el orden de cualquier otro elemento del grupo (porque son todos potencia de $g$).

Saludos.