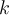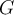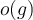Práctico 11 - Foro de consultas

Hola, buenas tardes.
El ejercicio es el siguiente:

La parte (a) la hice sin problemas. Me está costando un poco más la parte (b). Mi razonamiento hasta ahora es: 

Considere $3 \equiv 2^{k}$ $(mod$ $101)$ para algún $k \in \mathbb{Z}$.  (Válido porque 2 es raíz primitiva de U(101))
Entonces $2^{a} * 3^{b} \equiv 2^{a} * 2^{k*b}$ $(mod$ $101)$.
Luego, queremos hallar 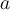$a$ y $b$ tales que $o(2^{a} * 3^{b}) = 50$,
$o(2^{a} * 3^{b}) = 50$ $\implies$ $(2^{a} * 3^{b})^{50} \equiv (2^{a} * 2^{k*b})^{50} \equiv 2^{50a} * 2^{50k*b} \equiv 2^{50(a+kb)} \equiv 1$ $(mod$ $101)$.

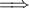
Pero la verdad a partir de ahí quede medio trancado... Hice algunos pasos más pero sin lograr resultados. ¿Alguna idea de si esta bien encaminado y como continuar?