Hola Valentín. Tu idea de la demostración está bien, tal vez le falte un poquito de formalidad. Para empezar, habría que fijar bien el punto 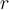 que te tomás al principio. Por ejemplo, podrías decir: "como
que te tomás al principio. Por ejemplo, podrías decir: "como 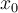 es frontera, en la bola de centro
es frontera, en la bola de centro 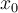 y radio 1 existe un punto
y radio 1 existe un punto  (ojo que ese punto no necesariamente es interior al conjunto). Luego, tomamos la bola de dentro
(ojo que ese punto no necesariamente es interior al conjunto). Luego, tomamos la bola de dentro 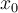 y radio
y radio  . De nuevo, como
. De nuevo, como 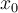 es frontera, existe en esa bola un punto
es frontera, existe en esa bola un punto  . Siguiendo este procedimiento construimos una sucesión de puntos tal que
. Siguiendo este procedimiento construimos una sucesión de puntos tal que  , por lo que
, por lo que  , y como por hipótesis el conjunto es cerrado por sucesiones teneomos que
, y como por hipótesis el conjunto es cerrado por sucesiones teneomos que  y por lo tanto
y por lo tanto 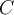 es cerrado".
es cerrado".
No es necesario separar la prueba entre puntos frontera aislados y no aislados, esta construcción funciona en ambos casos.
Saludos