Buenas! Tengo la curiosidad de saber si al demostrar la parte ( <-- ) del teorema, seria valido construir la sucesión de elementos de la siguiente forma:
Si el punto frontera x0 no es un punto aislado, tiene a su alrededor puntos interiores a C. Sea r cualquiera de estos puntos interiores a C. Se construye la sucesión
dividiendo la distancia entre r y x0 / 2. La distancia tendería a 0, y el limite de la sucesión seria x0.
Si por el contrario es aislado, r seria el mismo x0, y la sucesión y su limite serian medios triviales pero en teoría validos. La distancia seria constantemente 0 y el limite = x0.
El resto de la demostración sigue igual, mi duda era simplemente si construir la sucesión de esa manera seria correcto (y si seria necesario diferenciar en estos dos casos o no)
Saludos, Valentin
Demostracion de Proposicion 5.29. Pagina 87 de las notas
Número de respuestas: 1
En respuesta a Valentín Barrera Fourcade
Re: Demostracion de Proposicion 5.29. Pagina 87 de las notas
de Bernardo Marenco -
Hola Valentín. Tu idea de la demostración está bien, tal vez le falte un poquito de formalidad. Para empezar, habría que fijar bien el punto 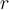 que te tomás al principio. Por ejemplo, podrías decir: "como
que te tomás al principio. Por ejemplo, podrías decir: "como 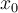 es frontera, en la bola de centro
es frontera, en la bola de centro 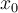 y radio 1 existe un punto
y radio 1 existe un punto  (ojo que ese punto no necesariamente es interior al conjunto). Luego, tomamos la bola de dentro
(ojo que ese punto no necesariamente es interior al conjunto). Luego, tomamos la bola de dentro 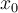 y radio
y radio  . De nuevo, como
. De nuevo, como 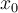 es frontera, existe en esa bola un punto
es frontera, existe en esa bola un punto  . Siguiendo este procedimiento construimos una sucesión de puntos tal que
. Siguiendo este procedimiento construimos una sucesión de puntos tal que  , por lo que
, por lo que  , y como por hipótesis el conjunto es cerrado por sucesiones teneomos que
, y como por hipótesis el conjunto es cerrado por sucesiones teneomos que  y por lo tanto
y por lo tanto 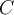 es cerrado".
es cerrado".
No es necesario separar la prueba entre puntos frontera aislados y no aislados, esta construcción funciona en ambos casos.
Saludos
