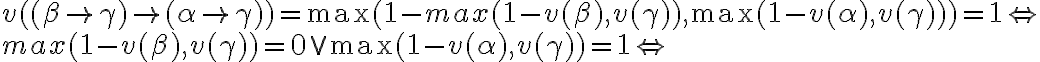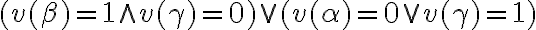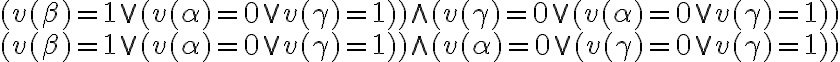SPOILERS
La premisa se hace verdadera cuando:
Que aplicando la distributiva repetidas veces nos da:
El último término es verdadero siempre, asique se puede ir, y nos queda que 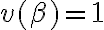 o
o 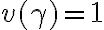 o
o 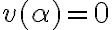 .
.
Por otro lado, la conclusión se hace verdadera cuando 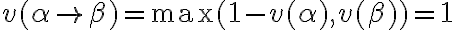 o lo que es lo mismo,
o lo que es lo mismo, 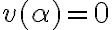 o
o 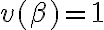 .
.
Queremos que siempre que la premisa sea verdadera, la conclusión sea verdadera.
En los casos en los que 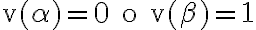 , se hacen verdadera tanto la premisa como la conclusión. ¿Pero que pasa cuando
, se hacen verdadera tanto la premisa como la conclusión. ¿Pero que pasa cuando 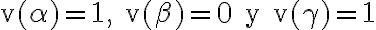 ? Se hace verdadera la premisa y no la conclusión. Queremos que esto no suceda. Queremos que
? Se hace verdadera la premisa y no la conclusión. Queremos que esto no suceda. Queremos que 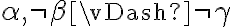 , o lo que es lo mismo, que cuando suceda
, o lo que es lo mismo, que cuando suceda 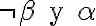 no suceda
no suceda 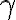 .
.
Dos ejemplos de fórmulas que cumplen esto son 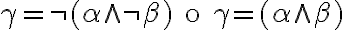 .
.
Saludos