Hola estoy intentando hacer este ejercico pero no entiendo bien la parte que dice i≠ gamma y i≠¬ gamma ( i≠ significa consecuencia logica ) puede pasar alguna vez esto? y si puede como hago para resolver el ejercicio!?
cualquier ayuda Gracias!
Hola estoy intentando hacer este ejercico pero no entiendo bien la parte que dice i≠ gamma y i≠¬ gamma ( i≠ significa consecuencia logica ) puede pasar alguna vez esto? y si puede como hago para resolver el ejercicio!?
cualquier ayuda Gracias!
por lo que entiendo me decis que la definicion de |= no me permite que se cumplan a la vez |≠ gamma y |≠ ¬ gamma entonces las afirmaciones son ambas falsas?
Lo que no puede darse a la vez es |= gamma y |= ¬ gamma, o sea que ambos sean verdaderos independiente de valuaciones (tautologías).
En cristiano, te dice "suponete que gamma de por sí no sabés si es verdadero o falso", y en esas condiciones tenés que pensar lo que sigue.
aaa...entiendo! entonces simplemente realizo la tabla de verdad para lo que me dan y busco un gamma?
Que te dice la definicion de |= ?
Que significa |/= gamma ? Y que significa |/= no gamma ?
Despues de tener eso resuelto podes decir, se pueden dar ambas cosas a la vez ? Si no se puede, porque, y si se puede, en que casos pasa.
Con respecto a lo último que decis, no entiendo a que tabla de verdad te referis, y además no te olvides que la tabla de verdad se puede hacer si conoces las formulas en cuestion con sus proposiciones, en este caso tenes variables que en principio no sabes que son.
creo que ya entendi, lo que me dice es : tome el valor que tome gamma
(gamma→ ß) → (alfa → gamma) es consecuencia logica de (alfa → ß) y lo que quise decir con tabla de "verdad" es que tomo los posibles valores que hacen 1 (alfa → ß) y con estos miro si (gamma→ ß) → (alfa → gamma) tambien toma el valor 1 para cualquier valor y si esto sucede puedo afirmar que es consecuencia logica.
Esta bien o tendria que hacer lo de maximo y minimo?
Yo tambien estoy con dudas en este ejercicio...
Si no entendi mal:
|/= gamma signifca que no existe una valuacion v tal que v(gamma)= 1
por lo que podes concluir de que v(gamma) = 0 porque por ser gamma perteneciente a PROP tiene un valor determinado en la valucion (sabes si es falsa o verdadera.)
Sabiendo que v(gamma)=0 entonces podes concluir que v(no gamma)=1
pero la otra hipotesis te dice que:
|/= no gamma y eso signifca que no existe una valuacion v tal que v(no gamma)=1
No se contradice ahi?La verdad no entiendo..
Si pudieran tirar un "pique" se agradece...
Saludos.
SPOILERS
La premisa se hace verdadera cuando:
Que aplicando la distributiva repetidas veces nos da:
El último término es verdadero siempre, asique se puede ir, y nos queda que 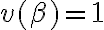 o
o 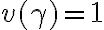 o
o 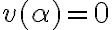 .
.
Por otro lado, la conclusión se hace verdadera cuando 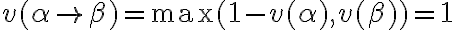 o lo que es lo mismo,
o lo que es lo mismo, 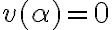 o
o 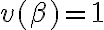 .
.
Queremos que siempre que la premisa sea verdadera, la conclusión sea verdadera.
En los casos en los que 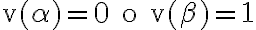 , se hacen verdadera tanto la premisa como la conclusión. ¿Pero que pasa cuando
, se hacen verdadera tanto la premisa como la conclusión. ¿Pero que pasa cuando 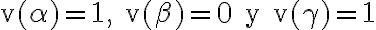 ? Se hace verdadera la premisa y no la conclusión. Queremos que esto no suceda. Queremos que
? Se hace verdadera la premisa y no la conclusión. Queremos que esto no suceda. Queremos que 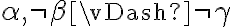 , o lo que es lo mismo, que cuando suceda
, o lo que es lo mismo, que cuando suceda 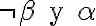 no suceda
no suceda 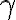 .
.
Dos ejemplos de fórmulas que cumplen esto son 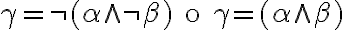 .
.
Saludos