Consultas

Buenas, estoy teniendo problemas para hallar la matriz de paridad a partir de una matriz generadora.

Por lo que entiendo de las notas del curso, para un código C(n,k) con matriz $G = [I_k | P]$ la matriz de chequeo de paridad es $H = [P^T | I_{n-k}]$.

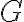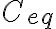Si $G$ no está escrita de esta forma, primero hay que hacer combinaciones lineales de filas y permutaciones de columnas para llegar a $G_{eq} = [I_k | P_{eq}]$, que es la matriz generadora de un código sistemático $C_{eq}$ equivalente a 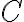$C$. Luego se puede hallar $H_{eq} = [P_{eq}^T | I_{n-k}]$

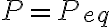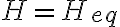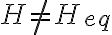Dudas: Se cumple que $P = P_{eq}$? $H = H_{eq}$? Si $H \neq H_{eq}$, cómo hallo 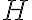$H$ a partir de $H_{eq}$?

Gracias de antemano!