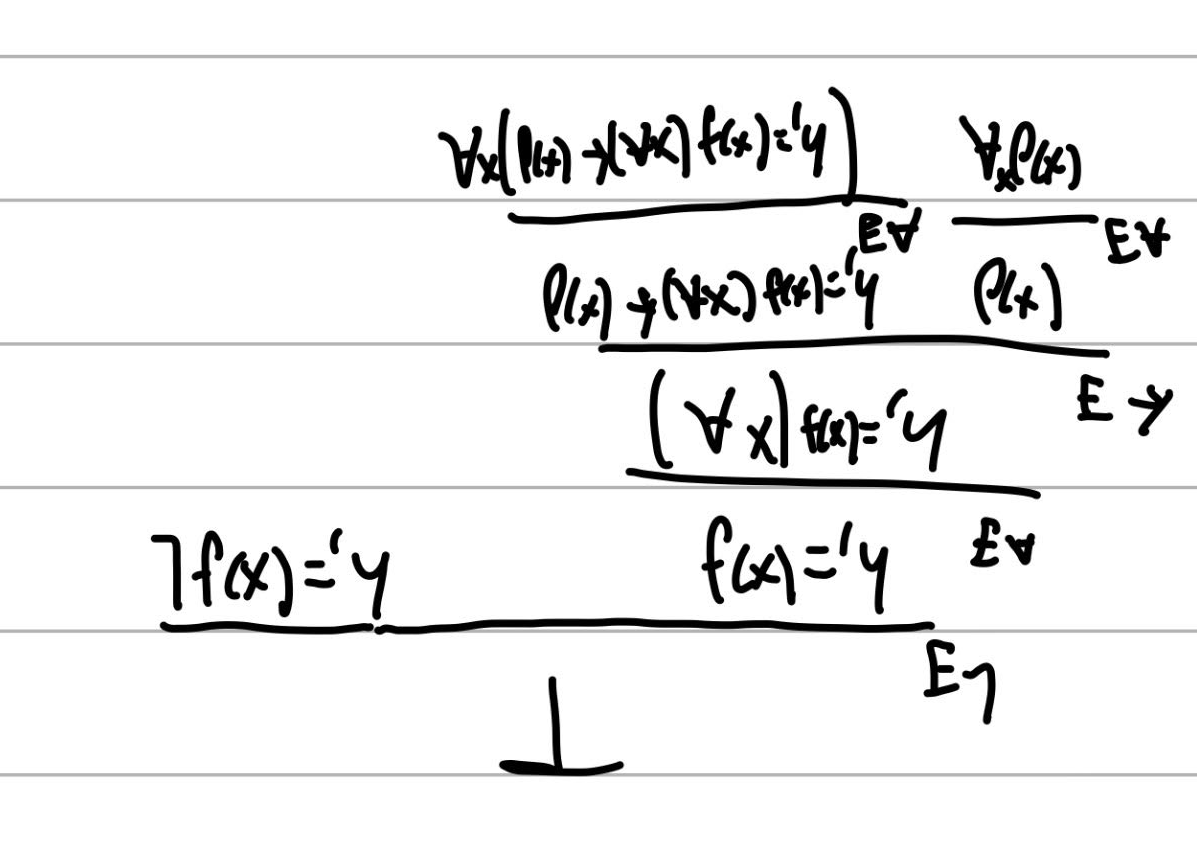
Buenas!, quería saber como podría resolverse esta derivación, intente varios caminos sin resultado, el que mas se acercó fue este(el primer para todo x en realidad es para todo y), pero tengo un problema en la parte izquierda, cuando intento hacer aparecer el existe para usar la primera hipótesis, siempre me queda una hipótesis con y libre y por lo tanto la derivación me queda invalida. Desde ya muchas gracias!.
Hola Agustín:
La contradicción hay que buscarla entre:
¬ x ='y que surge de la eliminación del existex ='y que se puede derivar con la segunda hipótesis.La segunda hipótesis nos permite deducir que todos los elementos del universo son iguales a f(x).
Esto a su vez nos permite derivar que dos términos a y b cualesquiera son iguales entre sí. Para ello hay que usar RI3 (transitiva):
(∀y) f(x) =' y
——————————————– E∀
f(x) =' a (∀y) f(x) = y
——————————————– RI2 ——————————————
a =' f(x) f(x) =' b
——————————————–——————————————–——– RI3
a =' b
De esa manera podés derivar x =' y que se contradice
con ¬ x =' y.
Espero que se entienda la sugerencia. Cualquier cosa volvé a preguntar.