TeoLeng: [Ejercicio 4] Simplificación

Hola!

Tengo una duda, cuando hay una gramatica que tiene una regla que es del estilo A -> A | e como es el caso de este:

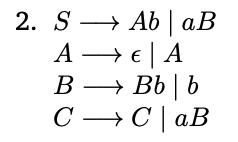
Cuando quiero simplificar usando por ejemplo la regla Eliminar unitarias entra en una especie de recursion, pero entiendo que una regla que se produzca a ella misma es innecesaria, esta bien eliminarla antes de aplicar los 4 pasos para simplificar la gramática?

En caso de que pueda, tendría que demostrar que produce lo mismo o simplemente basta con decir que como es una regla que se produce a ella misma sin sumar nada nuevo puedo eliminarla?

Gracias!

Re: [Ejercicio 4] Simplificación

de Diego Garat - lunes, 3 de junio de 2024, 21:40

hola:

según el algoritmo visto, al tratar a A->A, tendrías que agregar A->A (como parte de las posibles producciones de A) y luego quitarla del propio conjunto. más allá de que no tiene sentido, el resultado sería el mismo. recordá que P es un conjunto de producciones y, por lo tanto, no hay dos instancias repetidas de una misma producción. al agregar A->A sigue quedando el conjunto original y al final del paso de iteración que considera a A->A, se la borra de P.

saludos,
d.-

Re: [Ejercicio 4] Simplificación

de Nicolas Grosso San Roman - domingo, 7 de julio de 2024, 18:59

Hola. Una vez que ejecutamos ese paso y eliminamos A->A, qué sucede con la regla S->Ab? No encuentro una regla del algoritmo que me haga eliminar dicha regla. La eliminaría por intución de que la A no tiene producciones.

Re: [Ejercicio 4] Simplificación

de Santiago Gongora - lunes, 8 de julio de 2024, 17:06

Hola Nicolás,

Respuesta corta: se sacan todas las producciones que del lado derecho tengan una variable que no aparece en el lado izquierdo de ninguna producción ("una variable que no produce nada").

Respuesta larga: si hay una variable que no aparece nunca del lado izquierdo de una producción, quiere decir que esa variable "no produce nada". De alguna manera se podría decir que esa variable lo único que produce es el conjunto vacío (atención, me refiero a

$\emptyset$ y no a

$\{ \epsilon \}$ ).

Si lo único que produce "A" es el conjunto vacío, entonces la producción

$S \longrightarrow Ab$ equivale a

$S \longrightarrow \emptyset b$ y como el conjunto vacío es absorbente (análogo a la multiplicación por 0), entonces

$S \longrightarrow \emptyset$ . Es decir, S pasaría a generar al conjunto vacío (o sea, nada) y, por lo tanto, es lo mismo que la producción

$S \longrightarrow Ab$ ya no estuviera.

---------------------- 👁️ OJO 👁️ -------------------------

Por favor, al hacer este tipo de razonamientos tené en cuenta que cuando nos referimos a "una producción" nos estamos refiriendo a una única producción, con las restricciones descritas en la definición de GLC. Por ejemplo, si estás evaluando las producciones de Z y tenés

$Z \longrightarrow ccBc | ccX | abbaZ$ , en realidad ahí tenés 3 producciones, que tenés que analizar por separado:

---------------------- 👁️👄👁️ -------------------------

A las órdenes,
Santi