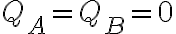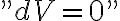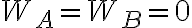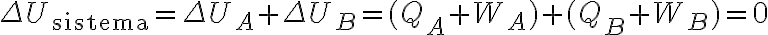Alexis, buenas noches. Me permito hacer un par de comentarios sobre lo que escribiste:
- Para aplicar las leyes de la termodinámica es necesario que previamente definamos las fronteras del sistema bajo estudio. Si bien las ecuaciones no cambian, esta definición puede afectar las magnitudes que intervienen (como la variación de la energía interna, el calor o el trabajo).
- Supongamos que el sistema "recipiente térmicamente aislado" es un termo. Definamos las fronteras del sistema como las paredes interiores del termo (todo lo que queda dentro de las fronteras lo llamaremos sistema, y lo que está por fuera, ambiente). Por ende, nuestro sistema son las sustancias agua en estado gaseoso (A) + agua en estado líquido (B).
- Como no hay transferencia de calor (desde el sistema hacia el ambiente o viceversa) por dicha frontera (ya que el sistema es adiabático), entonces los calores involucrados son nulos
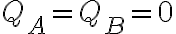
. Hago un paréntesis: ese es el calor que aparece en la expresión de la primera ley. El calor que se traspasa
por la frontera del sistema.
- El trabajo que está presente en la expresión de la primera ley, es el trabajo que (al igual que el calor) se transfiere
por la frontera del sistema. A este trabajo le llamamos trabajo de frontera y es el que definimos como la integral de P(V) en un proceso cuasiestático. Volviendo a nuestro modelo del sistema, el sistema no transfiere trabajo por su frontera dado que los sólidos y líquidos los consideramos incompresibles (su densidad es constante, y por ende
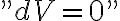
(puse esto último entre comillas para que se entienda la idea). Por lo tanto de esto último:
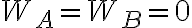
- Recién ahora aplicamos la primera ley con todo esta información:
Espero que haya quedado un poco más claro. Ante cualquier duda te invito a que consultes por aquí.
Saludos,
m
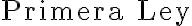que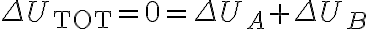 
(al ser sistema aislado se tiene que 
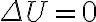) y sabiendo que 
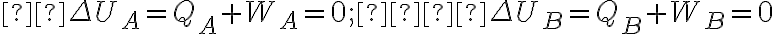, determinándose así que al ser un proceso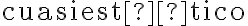 
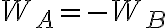. No entiendo cómo podemos determinar eso, o capaz hay que suponerlo de antemano. 