
En la segunda parte del inciso a-) el proceso BC puede ser adiabático porque de ser isotérmico mantendría las mismas temperaturas en B y C estando sobre una isoterma no?. De no ser esa la justificación entonces cuál sería?.

En la segunda parte del inciso a-) el proceso BC puede ser adiabático porque de ser isotérmico mantendría las mismas temperaturas en B y C estando sobre una isoterma no?. De no ser esa la justificación entonces cuál sería?.
 . Esto surge de combinar que el proceso sea cuasiestático + adiabático (su demostración la vamos a ver más adelante, cuando veamos la segunda ley de la termodinámica).
. Esto surge de combinar que el proceso sea cuasiestático + adiabático (su demostración la vamos a ver más adelante, cuando veamos la segunda ley de la termodinámica). dado que si
dado que si 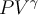 debe permanecer constante a lo largo de todo el proceso B-C, entonces va a cumplirlo para sus extremos (estados inicial y final).
debe permanecer constante a lo largo de todo el proceso B-C, entonces va a cumplirlo para sus extremos (estados inicial y final).Hola, los procesos adiabaticos cumplen PV^gamma=cte, con gamma=(grados de libertad +2)/ grados de libertad.
Los grados de libertad son 3 para monoatómico, 5 para diatómico y 6 para poliatomicos. Sin contar grados de vibración.
Saludos