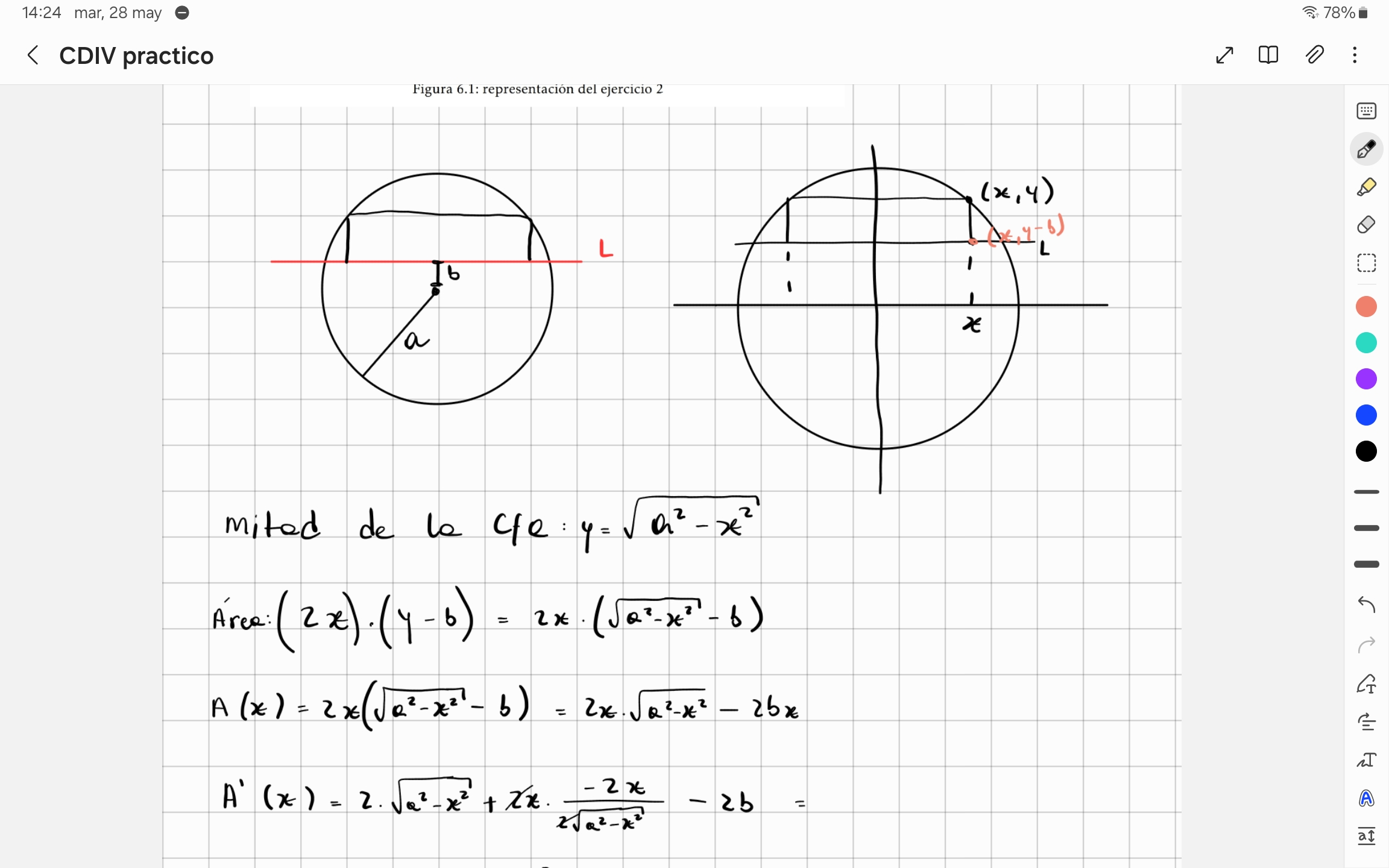
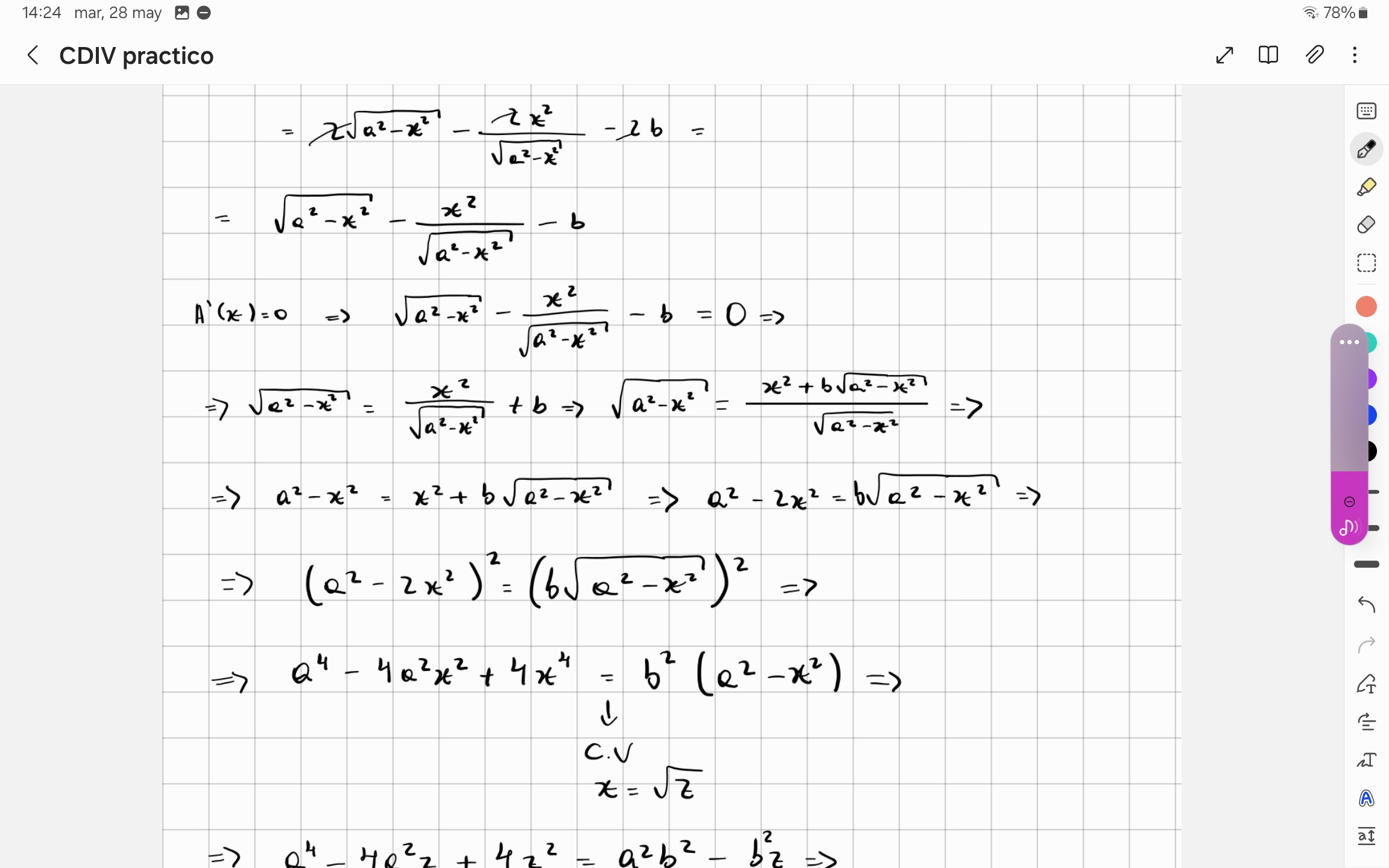Hola Julieta, la idea es correcta y por lo que vi en términos generales está bien lo que hiciste.
Lo que terminaste hallando es un candidato a extremo relativo (que debería ser máximo, habría que chequearlo), si quieres saber el valor del área máxima deberías evaluar en el valor de x en la función A(x).
Otra posibilidad, que creo que simplifica las cuentas es usar las funciones seno y coseno, ¿se te ocurre cómo?
Saludos, Florencia.