Foro Práctico 6

Hola. Una forma de probarlo es usando la desigualdad de Cauchy-Schwarz. Fijate que en este caso la norma está inducida por el producto interno usual en 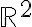$\mathbb{R}^2$. Es decir, si 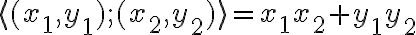$\langle (x_1,y_1);(x_2,y_2 )\rangle=x_1x_2+y_1y_2$ es el producto interno usual en 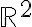$\mathbb{R}^2$, entonces la norma con la que estás trabajando puede verse como 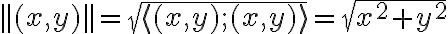$||(x,y)||=\sqrt{\langle (x,y);(x,y )\rangle}=\sqrt{x^2+y^2}$. La desigualdad de Cauchy-Schwarz dice que para cualquier producto interno se cumple la siguiente desigualdad con la norma inducida por ese producto interno:

$|\langle u ; v \rangle | \leq ||u|| ||v||$

Fijate entonces que $||u+v||^2 = \langle u+v ; u+v \rangle  = \langle u;u \rangle +2\langle u;v \rangle+\langle v;v \rangle = ||u||^2+2\langle u;v \rangle + ||v||^2$

Ahora, usando Cauchy-Schwarz, tenemos que 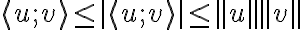$\langle u;v \rangle \leq |\langle u ; v \rangle | \leq ||u|| ||v||$, entonces:

$||u+v||^2 \leq  ||u||^2+2||u|| ||v|| + ||v||^2 = (||u|| + ||v||)^2$

Tomando raíz cuadrada se prueba la desigualdad triangular.

Saludos