Hola Agustina.
Por la gran cantidad de espacio en blanco en tu pregunta parece que hubieras querido incluír una foto o imagen sobre una parte específica.
Por la gran cantidad de espacio en blanco en tu pregunta parece que hubieras querido incluír una foto o imagen sobre una parte específica.
Si la pregunta es sobre todo el ejercicio, las propiedades 2,3, 7 se encuentran en las notas del eva.
Una forma fácil de probar las propiedades es apoyándose en lo que ya sabemos de matriz asociada.
Si fijas bases ortonormales A de V y B de W, y si llamas 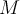 a la matriz asociada a T se puede probar que la matriz asociada a T* es
a la matriz asociada a T se puede probar que la matriz asociada a T* es  .
.
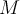 a la matriz asociada a T se puede probar que la matriz asociada a T* es
a la matriz asociada a T se puede probar que la matriz asociada a T* es  .
.Entonces si S y T son dos TL de V en W, sabemos que  , y como
, y como  (usamos que el conjugado de la suma es la suma de los conjugados y que la traspuesta de la suma es la suma de las traspuestas).
(usamos que el conjugado de la suma es la suma de los conjugados y que la traspuesta de la suma es la suma de las traspuestas).
 , y como
, y como  (usamos que el conjugado de la suma es la suma de los conjugados y que la traspuesta de la suma es la suma de las traspuestas).
(usamos que el conjugado de la suma es la suma de los conjugados y que la traspuesta de la suma es la suma de las traspuestas).Como fijadas las bases existe una biyección entre la TL y su matriz asociada, al tener que la matriz asociada a (S+T)*=S*+T* se llega a que lo mismo debe ocurrir a nivel de TL.
Razonando en forma similar se pueden demostrar las restantes propiedades.
En cuanto a la 1), es una de las consecuencias de usar una base ortonormal, se prueba que  , puedes encontrarlo en el teo. 121, p.89 del Libro Rojo.
, puedes encontrarlo en el teo. 121, p.89 del Libro Rojo.
 , puedes encontrarlo en el teo. 121, p.89 del Libro Rojo.
, puedes encontrarlo en el teo. 121, p.89 del Libro Rojo.Saludos
J.