Hola,
Bueno, voy con la parte (a). Dice "Sea impar tal que
impar tal que  . Probar que
. Probar que  es derivable en
es derivable en 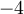 y calcular
y calcular  ".
".
La definición de función impar es que cumple para todo
para todo  . La definición de que
. La definición de que  es que
es que  .
.
Si querés probar que es derivable en
es derivable en 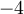 , entonces tenés que probar que el límite
, entonces tenés que probar que el límite  existe y es un número. Así que yo arrancaría con ese límite y trataría de que aparezca el otro que ya conocés, jugando con la definición de impar, y con algún cambio de variable.
existe y es un número. Así que yo arrancaría con ese límite y trataría de que aparezca el otro que ya conocés, jugando con la definición de impar, y con algún cambio de variable.
Bueno, voy con la parte (a). Dice "Sea
 impar tal que
impar tal que  . Probar que
. Probar que  es derivable en
es derivable en 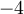 y calcular
y calcular  ".
".La definición de función impar es que cumple
 para todo
para todo  . La definición de que
. La definición de que  es que
es que  .
.Si querés probar que
 es derivable en
es derivable en 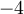 , entonces tenés que probar que el límite
, entonces tenés que probar que el límite  existe y es un número. Así que yo arrancaría con ese límite y trataría de que aparezca el otro que ya conocés, jugando con la definición de impar, y con algún cambio de variable.
existe y es un número. Así que yo arrancaría con ese límite y trataría de que aparezca el otro que ya conocés, jugando con la definición de impar, y con algún cambio de variable.Si precisás un poco más de spoiler, mirá lo que hago a continuación. Pero tratá de pensarlo un poco antes de ver.
Ahí ya está como para hacer un cambio de variable y que aparezca el otro límite.
