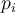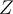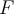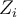MMC: Duda sesión 14, muestreo estratificado

Buenas ¿cómo están? Tengo una duda sobre esta transparencia:

de la penúltima ecuación se desprende que pi sería igual a dF(z)/dF_i y de la última que la suma de las p es 1, o sea que todas serían menores a 1 o a lo suma una p sería 1 y el resto 0. Lo que me genera duda es que yo entiendo que dF(z) es "más grande" que dF_i y por ende las p me quedarían mayores a 1. Obviamente asumo que estoy entendiendo mal, por eso la duda, me gustaría entender bien cómo se calculan esas p (que, por otra parte, intuitivamente parecen una probabilidad y luego en las transparencias siguientes se confirma ello).

Gracias desde ya.

Saludos

Re: Duda sesión 14, muestreo estratificado

de Ignacio Miguel Corrales Burutaran - jueves, 9 de mayo de 2024, 13:38

Seguramente alguien sepa y pueda responder esta consulta con mejor base que la mía, pero me permito contarte cómo lo razoné yo:
Las Fs que aparecen, son las funciones de densidad, no la función a integrar, esto es, la densidad del subconjunto dentro del cual estoy integrando en función del dominio total.
Por ejemplo, en el ejercicio entregable anterior, teníamos que cambiar el cálculo de la integral del cono, usando un muestreo que en vez de tomar puntos distribuidos en el cuadrado 1x1, tomaba puntos dentro de la circunferencia base del cono. Esto lo podés ver como que se partió al dominio Z en 2 subconjuntos: Z1 los puntos dentro de la circunferencia base y Z2 los puntos exteriores a dicha circunferencia.
el p1, para este caso concreto, lo calculamos como el área del circulo sobre el área total del cuadrado. Como vos decís, es una probabilidad.... la probabilidad de que tomando un punto al azar dentro del cuadrado 1x1, ese punto pertenezca al círculo. También es coherente con el cociente dF(z)/dF_i, ya que la densidad del sunconjunto Z1 (el círculo) es 1 sobre el área del círculo, y para Z (el cuadrado) va a ser 1 / área del cuadrado.

No sé si mi razonamiento es correcto y en caso de serlo, tampoco estoy seguro de que lo haya podido trasmitir medianamente bien.
Abrazo

Re: Duda sesión 14, muestreo estratificado

de Hector Cancela - jueves, 9 de mayo de 2024, 15:42

Buenas,

gracias Leandro por compartir tu duda, e Ignacio por tu respuesta, que está muy bien.

Como complemento, y para ayudar a pensarlo, puede ser útil tener en cuenta que los 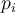$p_i$ efectivamente son probabilidades (la probabilidad que si tomo un punto al azar dentro de 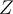$Z$ siguiendo la distribución 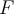$F$ , caiga dentro del subconjunto 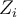$Z_i$ ). Visto de otra manera, se puede pensar que 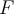$F$ es una función "de medida", que el tamaño de 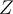$Z$ es 1, y que los 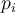$p_i$ son los "tamaños relativos" de los subconjuntos 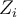$Z_i$ en relación a 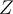$Z$ , siempre según la medida 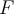$F$ . El conjunto 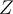$Z$ es nuestro conjunto universal, entonces su medida es 1; y está "partido" en varios 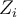$Z_i$ disjuntos, entonces la suma de los "tamaños" de los 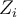$Z_i$ tiene que ser el total, es decir 1.

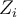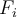Si luego vamos a hacer sorteos separados dentro de cada $Z_i$ , tenemos que generar una distribución de probabilidad específica para cada $i$ diferente. El método plantea tomar como distribución de probabilidad $F_i$ a la misma distribución 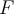$F$ restringida dentro del conjunto 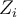$Z_i$ , para esto hay que normalizarla para que la probabilidad dentro de $i$ sea igual a uno. Esto es lo que se hace definiendo como densidad de probabilidad $dF_i(z)=F(z)/p_i$ .

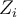Para un $z$ dado que pertenece a $Z_i$ , la probabilidad de que ese valor se elija si sorteo dentro de 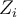$Z_i$ es mayor que si sorteo dentro de 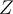$Z$ en general. Creo que esto es bastante intuitivo, 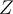$Z$ contiene a 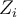$Z_i$ , por lo tanto hay más puntos donde elegir en 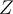$Z$ que en 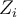$Z_i$ ; si yo sorteo restringido al subespacio $i$ , cada punto es más fácil que salga. Por lo tanto, $dF_i(z)$ va a ser mayor que $dF(z)$ , si $z$ pertenece a $Z_i$ . 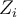Esto es coherente con la fórmula anterior, donde estamos dividiendo $F(i)$ por un número menor que 1, por lo cual el resultado va a ser mayor que el valor inicial.

Espero esto ayude/complemente los comentarios de Ignacio :).

Cualquier duda seguimos conversando. Saludos

Héctor