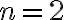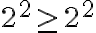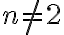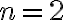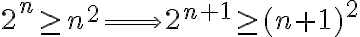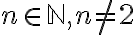Posible solución incorrecta

Posible solución incorrecta

de Thiago Podesta Ceschi -
Número de respuestas: 3

Hola, era para preguntar si es posible que en la pregunta "En un ejercicio de un examen se considera analizar..." no haya una respuesta correcta?

Las opciones de Duvija y Begoña me parecieron las que más se acercaban, pero durante el parcial descarté la opción de Begoña que había elegido inicialmente (la opción correcta según la solución), porque dice que para todo n distinto de 2 se cumple, pero después menciona que para n=0, 1, 2 también. Y ahora viendo la solución me doy cuenta que Duvija (la que yo elegí) también es incorrecta.

Aguardo respuesta, muchas gracias!

En respuesta a Thiago Podesta Ceschi

Re: Posible solución incorrecta

de Dionisio Fernández Pereira -
La opción de Begoña es correcta, no es lo mismo que el paso inductivo se cumpla para un n, a que la propiedad se cumpla para ese n.
El paso inductivo no se cumple para n=2 ya que eso implicaría P(3) lo cual es falso, pero P(2) es verdadero ya que 2^2\geq2^2.
En respuesta a Dionisio Fernández Pereira

Re: Posible solución incorrecta

de Geronimo De Leon Ramirez -
Buenas, Thiago, dos cosas.

Primero, si Begoña afirma que cierta propiedad sobre los naturales se cumple para n\neq 2 , y luego dice que también se cumple para n=2, no está diciendo nada contradictorio. Podrías decir que pudo haberse ahorrado palabras, pero no dijo nada falso: dijo que vale para distinto de 2, y luego dijo que también vale para dos. Es como el chiste de "Uno de los perros es mío...¿y el otro?...también".

Segundo, el tema es otro. Como dice Dionisio, lo que Begoña dice, y cito, es "El paso inductivo: 2^n\geq n^2 \Longrightarrow 2^{n+1}\geq (n+1)^2, vale para todo n\in \mathbb{N}, n\neq 2. Lo que ella está afirmando no es que la propiedad es cierta para todo natural distinto de 2, está afirmando que la proposición, el enunciado 2^n\geq n^2 \Longrightarrow 2^{n+1}\geq (n+1)^2 es cierto para todo n distinto de 2. Aquí sí está siendo precisa, porque ese enunciado puede ser demostrado para todo natural excepto para el 2, ya que ese enunciado (es una implicancia), para n=2, es falso.

Luego, se sigue que la respuesta correcta es la B.

Saludos.