Buenas tardes, me encuentro haciendo el ejercicio del parcial 2022 que se trata sobre moebius. En este se pide verificar si existe una transformación que lleve el plano superior a la bola unidad y a su vez lleve la recta Im{z}=Re{z} a la recta real. Deduje que no existe tal transformación, pero no se me ocurrió como demostrarlo a través de la sugerencia propuesta por la letra. Cuando leí la solución del problema no entendí que hacen.
En respuesta a Juan Mateo Sharoian Vartamian
Re: Solucion eje 1.1 del parcial del 2022
de Gabriel Mello -
Hola.
No sé qué más explicarte además de lo que ya dice la solución. Las transformaciones de moebius como todas las funciones holomorfas cuya derivada no se anula preservan ángulos. En particular si tal transformación existiera debería preservar el ángulo entre el eje real y la recta y=x, pero como muestra la solución eso no pasa.
Saludos,
Gabriel
No sé qué más explicarte además de lo que ya dice la solución. Las transformaciones de moebius como todas las funciones holomorfas cuya derivada no se anula preservan ángulos. En particular si tal transformación existiera debería preservar el ángulo entre el eje real y la recta y=x, pero como muestra la solución eso no pasa.
Saludos,
Gabriel
Buenas, yo tengo un problema sobre el mismo ejercicio.
No logro ver que el eje real y la circunferencia unidad formen 90 grados.
No logro ver que el eje real y la circunferencia unidad formen 90 grados.
En respuesta a Sofía Ferrando Bergeret
Re: Solucion eje 1.1 del parcial del 2022
Yo lo pensé así. La recta roja es Im(z)=Re(z) y forma un ángulo de 45° con el eje real. Despúes de aplicarle la transformación T pasa a ser el eje real, mientras que el eje real como se encuentra en el conjunto del semiplano superior pasa a B(0,1). Después el ángulo entre la recta y la circunferencia es el mismo que el de la recta y la tangente a la circunferencia en el punto donde se intersectan.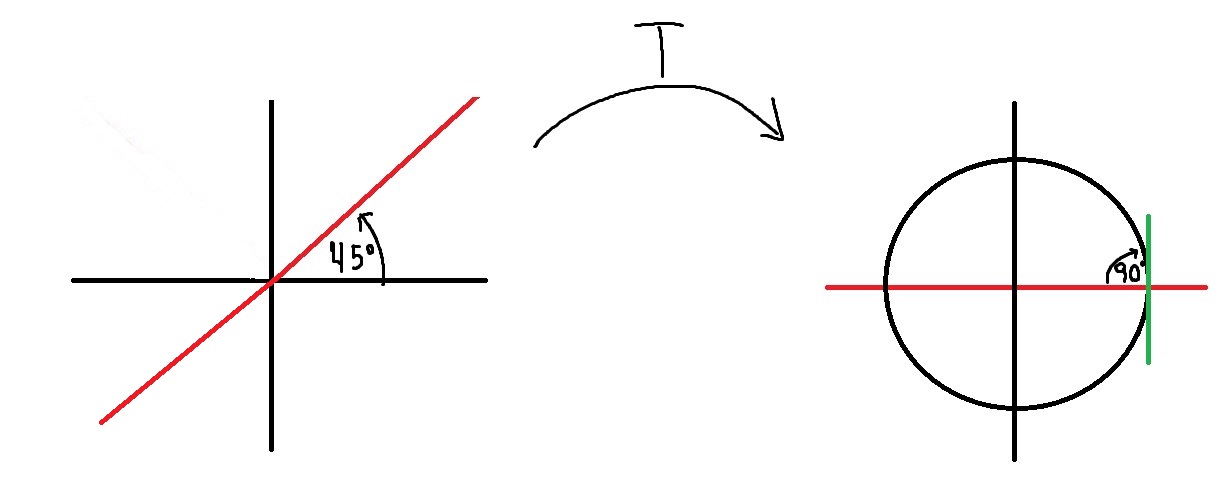
En respuesta a Pablo Zadkiel Alfano Patron
Re: Solucion eje 1.1 del parcial del 2022
de Gabriel Mello -
Es correcto.
Saludos,
Gabriel
Saludos,
Gabriel