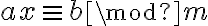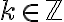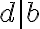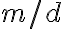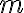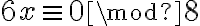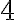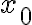Duda sobre división en congruencias

Duda sobre división en congruencias

de Marcela Pintos Nogues -
Número de respuestas: 2

Hola buenas tardes,

Tengo la siguiente duda sobre cuando hay que despejar un x en una congruencia (voy a utilizar el símbolo = para indicar congruencia):

Si yo tengo ax = b (mod m), entiendo que si mcd(a,m) = 1, busco el inverso de a mod m y multiplico en ambos lados para despejar x. Cuando d = mcd(a,m) > 1, divido todo entre el mcd(a,m) : ax/d = b/d (mod m/d) y ahí aplico lo anterior, pero no me queda claro qué pasa cuando b/d no es entero, en ese caso no hay solución?


En respuesta a Marcela Pintos Nogues

Re: Duda sobre división en congruencias

de Rodrigo Flores -

Buenas,

Fijate que si ax\equiv b \mod{m} tenés que para algún k\in \mathbb{Z}, b=ax + mk= d\dot{a}x+d\dot{m}k=d(\dot{a}x + \dot{m}k) por lo que solo hay solución si d|b. 

Hay que tener cuidado con que las soluciones que encontrás haciendo eso son únicas módulo m/d pero no módulo m, por ejemplo si querés resolver 6x\equiv 0 \mod{8},  x puede ser 0 o 4.

En general si x_0 es la solución módulo m/d todas van a ser de la forma x_0 + (m/d) k, donde k es un entero cualquiera.