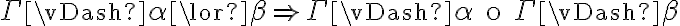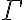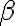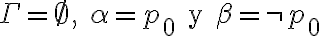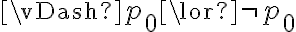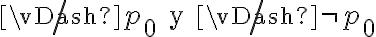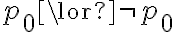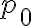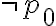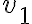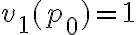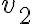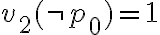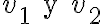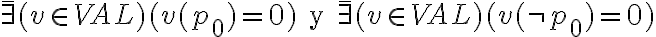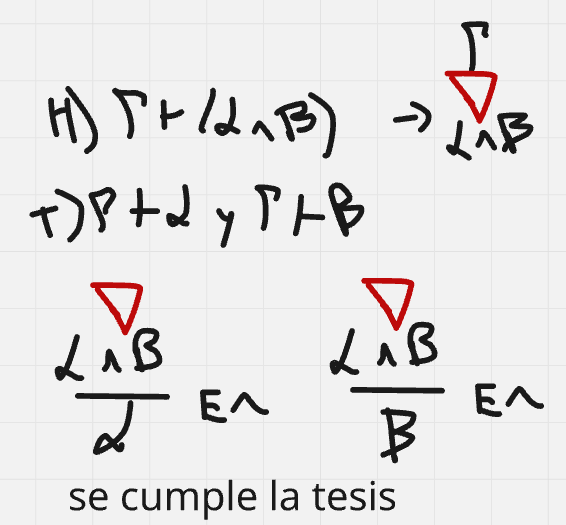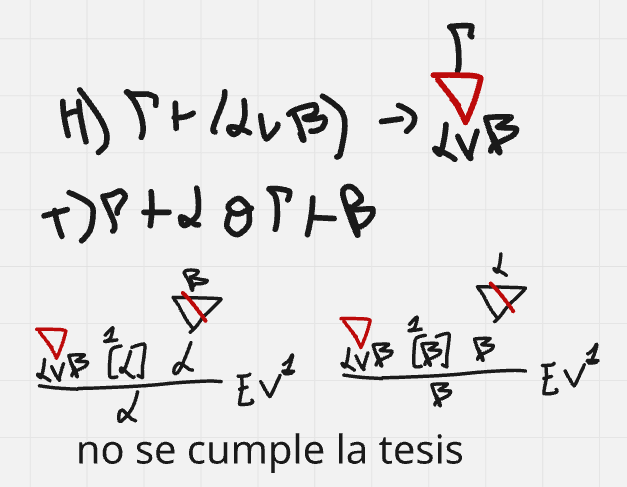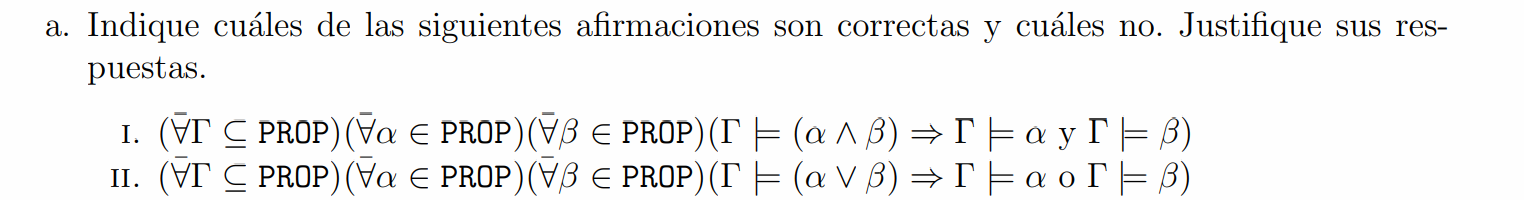
Hola buenas tardes, me queda la duda en este ejercicio porque es que no se cumple. entiendo la explicación, que no pueden ser tautologías ambas a la vez, pero no entiendo porque pasa a ser falso si es que el problema pone o que una es consecuencia semántica de gamma o la otra. La unica forma que se me ocurre es que cuando dice o alpha es consecuencia o beta es consecuencia, en vez de ser solo un o, también tendría que considerar el caso del y. Muchas gracias
Hola:
Para probar que (ii) es falsa, hay que encontrar Γ, α y β tales que:
El o se cumple cuando se cumple al menos una de las dos condiciones (es inclusivo).
Para que no se cumpla el o es necesario que no se cumpla ninguna de las dos condiciones.
Por lo tanto, tenemos que encontrar Γ, α y β que cumplan:
Es decir, Γ implica lógicamente la disyunción de α y β, pero no implica a α y β por separado.
Espero que aclare tu duda. Cualquier cosa, volvé a preguntar.
Buenas, yo también tengo una consulta de esta parte. También entiendo el argumento que usa la solución, pero traté de hacerlo directamente con definición directamente y no me estaría dando cuenta mi error o que estoy argumentando mal. Dejo foto abajo. Desde ya, muchas gracias!
Que tal:
Vos estás probando lo siguiente:
(∀v : Val) Si v(Γ) = 1 entonces v(α) = 1 o v(β) = 1
Pero lo que habría que probar es algo más fuerte:
(∀v : Val) (Si v(Γ) = 1 entonces v(α) = 1)
o
(∀v : Val) (Si v(Γ) = 1 entonces v(β) = 1)
Y esto no se puede probar porque no se cumple para todo Γ, α y β como lo muestra el contraejemplo de la solución.