Hola Alexis, en efecto tienes razón.
Desde el momento en que te dicen que lambda y mu son valores propios te están diciendo que primero tuvieron que ser raíces del polinomio característico, y si lambda es raíz doble (porque su ma=2) entonces mu debe ser raíz simple (su ma=1) porque el polinomio es de grado 3.
De hecho en la suma de las ma puedes poner el igual en lugar del menor o igual.
Pero está bien razonado y explicado.
Saludos
J.



 y como
y como 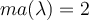 entonces tengo
entonces tengo 
 Por lo que sería cierta la afirmación
Por lo que sería cierta la afirmación