Hola, tengo una duda de la parte b de este ejercicio. En esta te piden comprobar que para que se de él movimiento planteado en el problema, la fuerza tiene que ser de la forma K/r^5. Lo que se me ocurrió es que para que eso suceda, se tiene que verificar la segunda ecuación de Binet, es decir que la fuerza sea proporcional a u^2(u+u´´) (saco el momento angular y la masa porque son constantes). Pero tuve una duda con respecto a eso, porque cuando planteo el momento angular, me doy cuenta de que este no es constante respecto a O, el polo de fuerzas. Esto ya que, por ejemplo, el radio en O vale 0, por lo que el momento angular es nulo, pero en el punto P tiene cierto radio y cierta velocidad por lo que no es nulo. No estaría entendiendo por que sucede esto, ¿no debería conservarse el momento angular si la fuerza neta es central? 
Hola Sebastián,
está muy bien la observación que hacés.
La idea en este ejercicio es evaluar el movimiento central hasta un instante antes de llegar a O.
El punto O queda fuera del alcance de nuestro estudio, ya que la fuerza no está bien definida para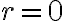 
. En todos los casos en que tenemos fuerzas que caen con potencias de 
nos encontramos con este problema.
Considerá la evolución del movimiento hasta un instante antes.
Saludos.