Buenas
Para entender este tipo de problemas una buena idea es siempre intentar pensar que pasa en los enteros, y luego en los primeros intervalos de la forma  para luego tratar de entender el límite. Sea
para luego tratar de entender el límite. Sea 
En este caso, para  entero no nulo como
entero no nulo como  tenemos que
tenemos que  . Tenemos entonces que
. Tenemos entonces que 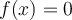 para todo
para todo  entero no nulo. Desde aqui ya se puede deducir que en caso de existir el limite de
entero no nulo. Desde aqui ya se puede deducir que en caso de existir el limite de  en
en 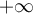 .
.
¿Que pasa con  en el intervalo [0,1)? ¿y en el intervalo [1,2)?
en el intervalo [0,1)? ¿y en el intervalo [1,2)?
Como  para todo
para todo  entonces
entonces  para todo
para todo 
Como  para todo
para todo  entonces
entonces  para todo
para todo 
Aqui tienes un bosquejo de como va qudando el gráfico.
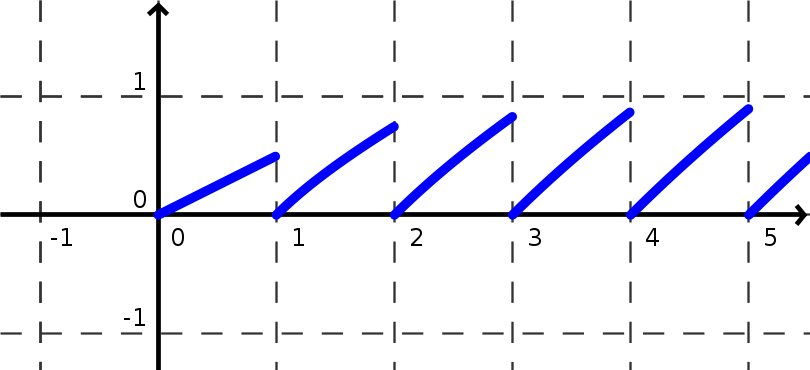
En realidad puedes probar que  para todo n natural no nulo.
para todo n natural no nulo.
Mas precisamente, para todo  entero no nulo tenemos que
entero no nulo tenemos que
Deducimos de esta forma que  no existe
no existe
Si tienes mas dudas vuelve a escribir
Saludos
