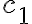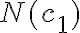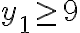No estoy pudiendo entender porque mi razonamiento esta mal en este ejercicio
En respuesta a Tomas Jorge Carrau Giacummo
Re: Ejercicio 1 parcial 2023 versión 1
En respuesta a Geronimo De Leon Ramirez
Re: Ejercicio 1 parcial 2023 versión 1
Muchas gracias
En respuesta a Tomas Jorge Carrau Giacummo
Re: Ejercicio 1 parcial 2023 versión 1
de Marcelo Lanzilotta -
Hola Tomás:
Todo el algoritmo está correcto, pero equivocaste la condición complementaria a y_1 (o bien y_2) menor o igual a 8.
El complemento es y_1 (o bien y_2) es mayor o igual a 9 (y pusiste 8).
Saludos
Marcelo
Todo el algoritmo está correcto, pero equivocaste la condición complementaria a y_1 (o bien y_2) menor o igual a 8.
El complemento es y_1 (o bien y_2) es mayor o igual a 9 (y pusiste 8).
Saludos
Marcelo
En respuesta a Marcelo Lanzilotta
Re: Ejercicio 1 parcial 2023 versión 1
Muchas gracias
En respuesta a Marcelo Lanzilotta
Re: Ejercicio 1 parcial 2023 versión 1
Hola, que tal?. Yo estoy con el mismo ejercicio hace días.
Sí bien tengo el algoritmo y las condiciones correctas, no logro dar con el resultado.
Es el número total de soluciones menos la condición c1 menos la condición c2 y no logro dar con el resultado.
Sí bien tengo el algoritmo y las condiciones correctas, no logro dar con el resultado.
Es el número total de soluciones menos la condición c1 menos la condición c2 y no logro dar con el resultado.
El resultado me da 648. Sí pueden darme una guía lo agradecería mucho, saludos.
En respuesta a Geronimo Manuel Mora Acosta
Re: Ejercicio 1 parcial 2023 versión 1
de Mauricio Guillermo -
Hola,
Buenas noches. No puedo imaginar en qué te estás equivocando. Este problema tiene una acotación por abajo en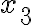 y para
y para 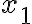 y
y 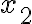 tenés acotaciones por arriba también. Lo primero es trasladar
tenés acotaciones por arriba también. Lo primero es trasladar 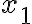 y
y 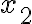 para llevar todo a un problema en
para llevar todo a un problema en 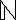 . El cambio de variables
. El cambio de variables 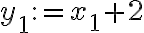 e
e 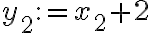 hace ese trabajo. Esto te cambia las cotas superiores también, verbigracia
hace ese trabajo. Esto te cambia las cotas superiores también, verbigracia 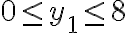 (ídem con
(ídem con 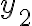 ). Ahora te queda transformar la condición
). Ahora te queda transformar la condición 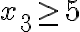 en algo manejable y para eso el cambio de variables que funciona es
en algo manejable y para eso el cambio de variables que funciona es 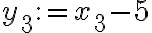 .
.
La ecuación en las nuevas variables te queda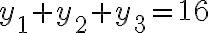 con las condiciones
con las condiciones 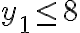 e
e 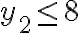 (y las 3 naturales, claro). Eso corresponde a las primeras líneas de la solución de Tomás Carrau (ver arriba).
(y las 3 naturales, claro). Eso corresponde a las primeras líneas de la solución de Tomás Carrau (ver arriba).
Luego lo que falta es aplicar inclusión/exclusión. Recuerda que este método te lleva a calcular soluciones que cumplen las condiciones complementarias (por eso es útil acá). Es decir,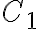 son las soluciones que tienen
son las soluciones que tienen 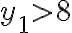 y
y 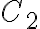 las que tienen
las que tienen 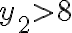 . Mira por favor el hilo de la discusión porque es justamente lo que Gerónimo y Marcelo explicaron. La solución de Carrau está casi bien, módulo las aclaraciones que le hicieron los colegas.
. Mira por favor el hilo de la discusión porque es justamente lo que Gerónimo y Marcelo explicaron. La solución de Carrau está casi bien, módulo las aclaraciones que le hicieron los colegas.
Cordiales saludos,
Mauricio Guillermo
(responsable del teórico virtual nocturno).
Buenas noches. No puedo imaginar en qué te estás equivocando. Este problema tiene una acotación por abajo en
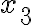 y para
y para 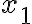 y
y 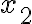 tenés acotaciones por arriba también. Lo primero es trasladar
tenés acotaciones por arriba también. Lo primero es trasladar 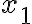 y
y 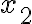 para llevar todo a un problema en
para llevar todo a un problema en  . El cambio de variables
. El cambio de variables 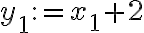 e
e 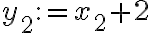 hace ese trabajo. Esto te cambia las cotas superiores también, verbigracia
hace ese trabajo. Esto te cambia las cotas superiores también, verbigracia 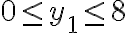 (ídem con
(ídem con 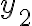 ). Ahora te queda transformar la condición
). Ahora te queda transformar la condición 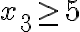 en algo manejable y para eso el cambio de variables que funciona es
en algo manejable y para eso el cambio de variables que funciona es 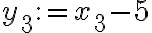 .
. La ecuación en las nuevas variables te queda
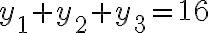 con las condiciones
con las condiciones 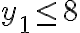 e
e 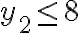 (y las 3 naturales, claro). Eso corresponde a las primeras líneas de la solución de Tomás Carrau (ver arriba).
(y las 3 naturales, claro). Eso corresponde a las primeras líneas de la solución de Tomás Carrau (ver arriba). Luego lo que falta es aplicar inclusión/exclusión. Recuerda que este método te lleva a calcular soluciones que cumplen las condiciones complementarias (por eso es útil acá). Es decir,
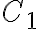 son las soluciones que tienen
son las soluciones que tienen 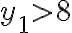 y
y 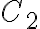 las que tienen
las que tienen 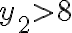 . Mira por favor el hilo de la discusión porque es justamente lo que Gerónimo y Marcelo explicaron. La solución de Carrau está casi bien, módulo las aclaraciones que le hicieron los colegas.
. Mira por favor el hilo de la discusión porque es justamente lo que Gerónimo y Marcelo explicaron. La solución de Carrau está casi bien, módulo las aclaraciones que le hicieron los colegas.Cordiales saludos,
Mauricio Guillermo
(responsable del teórico virtual nocturno).